
【题目】综合与实践:
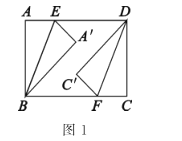
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,将
,将![]() 分别沿
分别沿![]() 折叠,点
折叠,点![]() 分别落在点
分别落在点![]() 处.
处.
探究展示:(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() (依据1)
(依据1)
∴![]() ,
,
∴![]() (依据2)
(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:(2)如图2,折叠过程中,当点![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 中,则四边形
中,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
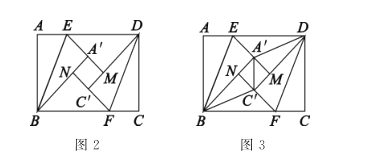
联想拓广:(3)如图3,连接![]() ,
,
①当![]() 时,
时,![]() 的长为_____________________;
的长为_____________________;
②![]() 的长有最小值吗?若有,请你直接写出
的长有最小值吗?若有,请你直接写出![]() 的最小值;若没有,请说明理由.
的最小值;若没有,请说明理由.
【答案】(1)①两直线平行,内错角相等;同位角相等,两直线平行;②详见解析;(2)四边形![]() 是矩形,详见解析;(3)①
是矩形,详见解析;(3)①![]() ,②
,②![]() 的长有最小值,最小值为2,理由见详解.
的长有最小值,最小值为2,理由见详解.
【解析】
(1)①填写相应的平行线的性质及判定定理即可;
②利用一组对边平行且相等证得四边形![]() 是平行四边形即可;
是平行四边形即可;
(2)延长![]() ,交
,交![]() 于点
于点![]() ,由对折可知,
,由对折可知,![]() ,进而可证得
,进而可证得![]() ,同理,
,同理,![]() ,再由(1)得
,再由(1)得![]() ,几何折叠性质可得
,几何折叠性质可得![]() ,利用等角的余角相等可得
,利用等角的余角相等可得![]() ,进一步得到
,进一步得到![]() ,最终证得
,最终证得![]() ,最后利用有三个角是直角的四边形是矩形可得四边形
,最后利用有三个角是直角的四边形是矩形可得四边形![]() 是矩形;
是矩形;
(3)①延长![]() 交BC于点H,反向延长
交BC于点H,反向延长![]() 交AD于点K,可证得BH=
交AD于点K,可证得BH=![]() BC=4,进而求得
BC=4,进而求得![]() ,从而可求得
,从而可求得![]() ,最后设AE=
,最后设AE=![]() E=x,在Rt△
E=x,在Rt△![]() 中,利用勾股定理求得x的值即可;
中,利用勾股定理求得x的值即可;
②连接BD交![]() 于点O,通过证四边形
于点O,通过证四边形![]() 为平行四边形可得OB=OD=5,
为平行四边形可得OB=OD=5,![]() ,当点
,当点![]() 、
、![]() 与点B、D共线时,
与点B、D共线时,![]() 的长可取得最小值,由此可得结果.
的长可取得最小值,由此可得结果.
解:(1)①“依据1”指两直线平行,内错角相等;
“依据2”指同位角相等,两直线平行;
②证明:在矩形![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,且
,且![]() ;
;
(2)四边形![]() 是矩形,
是矩形,
证明:延长![]() ,交
,交![]() 于点
于点![]() ,如下图,
,如下图,
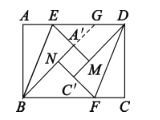
由对折可知,![]() ,
,
∵![]() ,
,
∴![]() ,
,
同理,![]() ,
,
由(1)得,![]() ,
,
∴![]() ,
,
由对折可知,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在矩形![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(3)①如图,延长![]() 交BC于点H,反向延长
交BC于点H,反向延长![]() 交AD于点K,
交AD于点K,
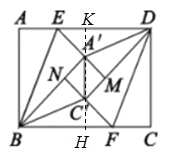
∵![]() ,AB∥CD,AD∥BC,∠A=∠C=90°,
,AB∥CD,AD∥BC,∠A=∠C=90°,
∴四边形ABHK和CDKH均为矩形,
∴AK=BH,KD=CH,KH=AB=6,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴KD=BH,
∴AK=KD=BH =![]() AD=4,
AD=4,
在Rt![]() 中,
中,![]()
∴![]() ,
,
设AE=![]() E=x,则EK=4-x,
E=x,则EK=4-x,
在Rt![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴AE=![]() ;
;
②如图,连接BD交![]() 于点O,
于点O,
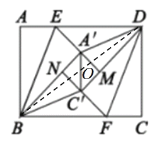
由(2)得四边形![]() 是矩形,
是矩形,
∴![]() ∥
∥![]() ,
,
又∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴OB=OD,![]() ,
,
∵在Rt△ABD中,BD=![]() ,
,
∴OB=OD=5,
又∵![]() 6,
6,
∴当点![]() 、B、O不共线时
、B、O不共线时![]() >
>![]() ,
,
即![]() >6-5,
>6-5,![]() >1,
>1,
当点![]() 、B、O共线时,
、B、O共线时,![]() =
=![]() ,
,
即![]() =6-5,
=6-5,![]() =1,
=1,
∴![]() 取得最小值,最小值为1,
取得最小值,最小值为1,
又∵![]() ,
,
∴![]() 取得最小值,最小值为2.
取得最小值,最小值为2.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
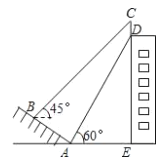
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格图中建立平面直角坐标系,![]() 的顶点坐标为
的顶点坐标为![]() 、
、![]() 、
、![]() .
.
(1)若将![]() 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的![]() ;
;
(2)画出![]() 绕C1顺时针方向旋转90°后得到的
绕C1顺时针方向旋转90°后得到的![]() ;
;
(3)![]() 与
与![]() 是中心对称图形,请写出对称中心的坐标: ;并计算
是中心对称图形,请写出对称中心的坐标: ;并计算![]() 的面积: .
的面积: .

查看答案和解析>>
科目:初中数学 来源: 题型:
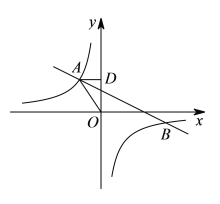
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() 若点
若点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() ,下列选项正确的有( )
,下列选项正确的有( )
①![]() ;②
;②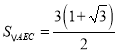 ;③
;③![]() ;④
;④![]()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为边作等腰直角
为边作等腰直角![]() ,其中
,其中![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
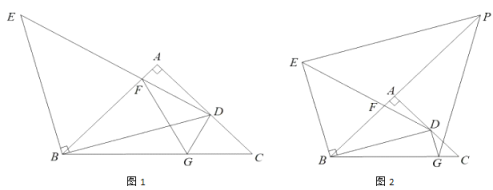
(1)如图1,若![]() ,连接
,连接![]() .
.
①若![]() ,求
,求![]() 的长度;
的长度;
②求证:![]() ;
;
(2)如图2,若![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,请猜想线段
,请猜想线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与直线
与直线![]() (
(![]() 为常数
为常数![]() ,)交于A,B两点,直线
,)交于A,B两点,直线![]() 交
交![]() 轴于点C,点A的坐标为
轴于点C,点A的坐标为![]() ;
;
(1)若![]() ,则A点的坐标为__________,点B的坐标为____________
,则A点的坐标为__________,点B的坐标为____________
(2)已知点![]() ,抛物线
,抛物线![]() 与线段
与线段![]() 有两个公共点,求
有两个公共点,求![]() 的取值范围;
的取值范围;
(3)①如图1,求证: ![]()
②如图2,设抛物线的顶点为F,直线![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,直线
,直线![]() (
(![]() 为常数
为常数![]() ,)经过点A,并交抛物线的对称轴于点E,若
,)经过点A,并交抛物线的对称轴于点E,若![]() (
(![]() 为常数)则
为常数)则![]() 的值是否发生变化?若不变,请求出
的值是否发生变化?若不变,请求出![]() 的值;若变化,请说明理由.
的值;若变化,请说明理由.
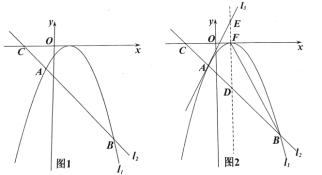
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com