
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() 若点
若点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() ,下列选项正确的有( )
,下列选项正确的有( )
①![]() ;②
;②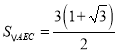 ;③
;③![]() ;④
;④![]()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】C
【解析】
①连结OE,根据正方形性质和等边三角形性质可证:OE垂直平分AD,进而可证:△CDF∽△EOF,由相似三角形性质即可求得DF;
②由![]() ,又由两条平行之间的距离处处相等得
,又由两条平行之间的距离处处相等得![]() ,即可得
,即可得![]() ,利用三角形面积公式计算即可得出结果;
,利用三角形面积公式计算即可得出结果;
③过点F作PQ⊥CD分别交CD、AB于点P、Q,在MA上截取MT=MC,连接FT、CT,求得相关的线段长,可证:△MCF≌△MTF(SAS),Rt△CFP≌Rt△FTQ(HL),求出BT的长,利用特殊角的三角函数值和等边三角形的判定与性质即可求得![]() ;
;
④根据解直角三角形和线段的加减运算分别求出![]() 的长,整理即可得出这三条线段之间的数量关系,即可做出判断.
的长,整理即可得出这三条线段之间的数量关系,即可做出判断.
解:如图1,连结OE,

∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠ADC=∠DAB=90°,OD=OB,OC=OA,BD=AC,
∴OD=OB=OC=OA,
∵△ADE是等边三角形,![]() ,
,
∴![]() ,∠ADE=60°,
,∠ADE=60°,
∴![]() ,
,
∴![]() ,
,
则![]() ,
,
∵AE=DE,OD=OA,
∴OE垂直平分AD,即OE⊥AD,DH=AH![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∵∠ADC=∠DHE=90°,
∴CD∥OE,
∴△CDF∽△EOF,
∴![]() ,则
,则![]() ,即
,即![]() ,
,
∵![]() ,则
,则![]() ,
,
∴![]() ,解得:
,解得:![]() ,故①正确;
,故①正确;
∵![]() ,
,
又∵CD∥OE,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
故②正确;
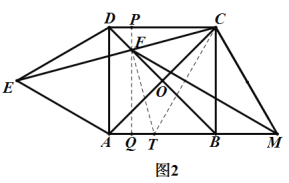
如图2,过点F作PQ⊥CD分别交CD、AB于点P、Q,在MA上截取MT=MC,连接FT、CT,则![]() 为等腰三角形,
为等腰三角形,
在![]() 中,
中,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
由![]() 得:
得:![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,
∴![]() ,则
,则![]() ,
,
![]() ,
,
∵FM平分∠AMC,
∴∠CMF=∠AMF,
在△MCF和△MTF中,
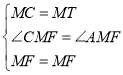 ,
,
∴△MCF≌△MTF(SAS),
∴CF=FT,
在Rt△CFP和Rt△FTQ中,
![]()
∴Rt△CFP≌Rt△FTQ(HL),
∴![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,则
,则![]() 为等边三角形,
为等边三角形,
∴![]() ,故③正确;
,故③正确;
∵![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]() ,
,
∵![]()
∴![]() ,故④错误;
,故④错误;
∴正确的选项有3个,
故选:C.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】国家计划2035年前实施新能源汽车,某公司为加快新旧动能转换,提高公司经济效益,决定对近期研发出的一种新型能源产品进行降价促销.根据市场调查:这种新型能源产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个新型能源产品的成本为100元.
问:(1)设该产品的销售单价为![]() 元,每天的利润为
元,每天的利润为![]() 元.则
元.则![]() _________(用含
_________(用含![]() 的代数式表示)
的代数式表示)
(2)这种新型能源产品降价后的销售单价为多少元时,公司每天可获利32000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
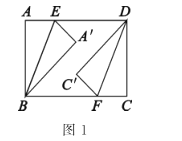
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,将
,将![]() 分别沿
分别沿![]() 折叠,点
折叠,点![]() 分别落在点
分别落在点![]() 处.
处.
探究展示:(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() (依据1)
(依据1)
∴![]() ,
,
∴![]() (依据2)
(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:(2)如图2,折叠过程中,当点![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 中,则四边形
中,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
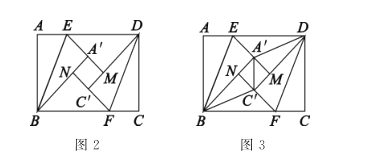
联想拓广:(3)如图3,连接![]() ,
,
①当![]() 时,
时,![]() 的长为_____________________;
的长为_____________________;
②![]() 的长有最小值吗?若有,请你直接写出
的长有最小值吗?若有,请你直接写出![]() 的最小值;若没有,请说明理由.
的最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
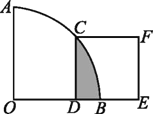
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com