
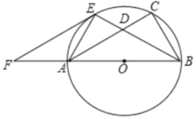
【题目】如图,已知以![]() 的边
的边![]() 为直径作
为直径作![]() 的外接圆的
的外接圆的![]() 平分线
平分线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)求证:![]() 是
是![]() 切线;
切线;
(2)若![]() 求
求![]() 的长.
的长.
【答案】(1)见详解;(2)![]()
【解析】
(1)要证EF是 ![]() 的切线,只要连接OE,再证∠FEO=90°即可;
的切线,只要连接OE,再证∠FEO=90°即可;
(2)证明△FEA∽△FBE,得出![]() ,从而得到AF的值,进而得到
,从而得到AF的值,进而得到![]() ,结合勾股定理得到关于AE的方程,即可求出AE的长.
,结合勾股定理得到关于AE的方程,即可求出AE的长.
(1)连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠OBE,
∵EF∥AC,
∴∠CAE=∠FEA,
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB,
∵AB是![]() 的直径,
的直径,
∴∠AEB=90°,
∴∠FEO=90°,
∴EF是![]() 切线;
切线;
(2)∵∠FEA=∠OEB=∠OBE,∠F=∠F,
∴FEA~FBE,
∴![]() ,
,
即:![]() ,
,
∴AF×(AF+15)=10×10,解得:AF=5或AF=-20(舍去),
∴![]() ,
,
∵在RtABE中,AE2+BE2=AB2,
∴AE2+(2AE)2=152,
∴AE=![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
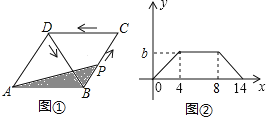
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )
A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
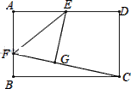
【题目】如图,矩形 ABCD 中,AB=8,BC=12,E 为 AD 中点,F 为 AB 上一点,将△ AEF 沿 EF 折叠后,点 A 恰好落到 CF 上的点 G 处,则折痕 EF 的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=![]() :7;④FB2=OFDF.其中正确的是( )
:7;④FB2=OFDF.其中正确的是( )
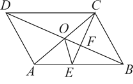
A.①②④B.①③④C.②③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
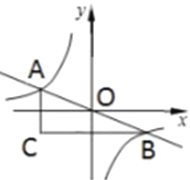
【题目】如图,在平面直角坐标系中,过原点的直线与反比例函数![]() 交于点
交于点![]() ,与反比例函数
,与反比例函数 ![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,过点
轴的垂线,过点![]() 作
作![]() 轴的垂线,两直线交于点
轴的垂线,两直线交于点![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识回顾]
七年级学习代数式求值时,遇到这样一类题 “代数式![]() 的值与
的值与![]() 的取值无关,求
的取值无关,求![]() 的值”,通常的解题方法是:把
的值”,通常的解题方法是:把![]() 看作字母,
看作字母,![]() 看作系数合并同类项,因为代数式的值与
看作系数合并同类项,因为代数式的值与![]() 的取值无关,所以含
的取值无关,所以含![]() 项的系数为
项的系数为![]() ,即原式
,即原式![]() ,所以
,所以![]() ,则
,则![]() .
.
[理解应用]
![]() 若关于
若关于![]() 的多项式
的多项式![]() 的值与
的值与![]() 的取值无关,试求
的取值无关,试求![]() 的值:
的值:
![]() 若一次函数
若一次函数![]() 的图像经过某个定点,则该定点坐标为 ;
的图像经过某个定点,则该定点坐标为 ;
[能力提升]
![]() 张如图1的小长方形,长为
张如图1的小长方形,长为![]() ,宽为
,宽为![]() ,按照图2方式不重叠地放在大矩形
,按照图2方式不重叠地放在大矩形![]() 内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为
内,大矩形中未被覆盖的两个部分(图中阴影部分) ,设右上角的面积为![]() ,左下角的面积为
,左下角的面积为![]() ,当
,当![]() 的长变化时,
的长变化时,![]() 的值始终保持不变,求
的值始终保持不变,求![]() 与
与![]() 的等量关系.
的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
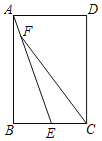
【题目】如图,在矩形ABCD中,点E是BC上一点,连接AE,点F是AE上一点,连接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC.
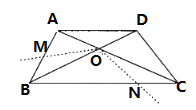
(1)求出sin∠DBC的值;
(2)若AD=2,把∠BOC绕点O顺时针旋转![]() (
(![]() ),交AB于点M,交BC于点N(如图),求证:四边形OMBN的面积为一个定值,并求出这个定值.
),交AB于点M,交BC于点N(如图),求证:四边形OMBN的面积为一个定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com