
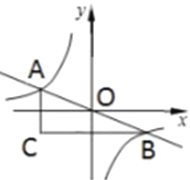
【题目】如图,在平面直角坐标系中,过原点的直线与反比例函数![]() 交于点
交于点![]() ,与反比例函数
,与反比例函数 ![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,过点
轴的垂线,过点![]() 作
作![]() 轴的垂线,两直线交于点
轴的垂线,两直线交于点![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() 的值为_______.
的值为_______.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种型号的商品。每件甲种商品的进价比每件乙种商品的进价少2元,且用80元购进甲种商品的数量与用100元购进乙种商品的数量相同.
(1)求甲、乙两种商品每件的进价各为多少元;
(2)每件甲种商品售价为12元,每件乙种商品售价为15元,该超市本次购进甲种商品的数量比购进乙种商品的数量的3倍少5件,要使两种商品全部售出后所获总利润超过371元,求该超市本次至少购进乙种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)
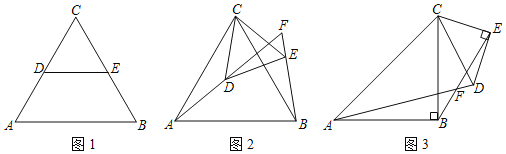
(1)如图1,已知△CAB和△CDE均为等边三角形,D在AC上,E在CB上,易得线段AD和BE的数量关系是 .
(2)将图1中的△CDE绕点C旋转到图2的位置,直线AD和直线BE交于点F.
①判断线段AD和BE的数量关系,并证明你的结论;
②图2中∠AFB的度数是 .
(探究拓展)
(3)如图3,若△CAB和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F,分别写出∠AFB的度数,线段AD、BE间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,AB是⊙O的一条弦,AP是⊙O的切线.作BM=AB并与AP交于点 M,延长MB交AC于点E,交⊙O于点D,连接AD、BC.

(1)求证:AB=BE;
(2)若BE=3,OC=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题:
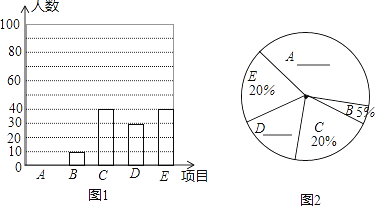
(1)在这项调查中,共调查了_______名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
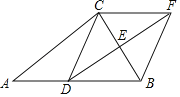
【题目】在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,过点C作CF∥AB,与DE的延长线并交于点F,连接BF.
(1)试判断四边形CDBF的形状,并说明理由;
(2)若CD=5,sin∠CAB=![]() ,过点C作CH⊥BF,垂足为H点,试求CH的长.
,过点C作CH⊥BF,垂足为H点,试求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
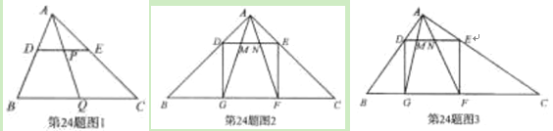
【题目】(本题满分10分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:![]() .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com