
����Ŀ��Ϊ��ǿѧ�����������ijУ��չ��������μ������ѧУ������ѧ���п���A������B��������Զ��C��������D���ܲ���E���������ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ��ʾ������ͳ��ͼ������ͼ�е���Ϣ����������⣺
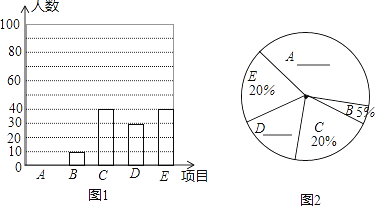
��1������������У���������_______��ѧ����
��2���뽫����ͳ��ͼ����������
��3������У��1200����Уѧ���������ϲ�������ѧ����Լ�ж����ˣ�
���𰸡�*1��200����2����ͼ����������3��240�ˣ�
�����������������
��1����ͼ1�ɵ�ϲ����B���˶�������10�ˣ���ͼ2�ɵ�ϲ����B���˶�����ռ������5%����10��5%�������������Ϊ200�ˣ�
��2������ͼ1��֪ϲ��B��C��D��E�����˶��������ֱ�Ϊ10��40��30��40�ˣ��ɴ˿ɵ�ϲ��A���˶�������Ϊ��200-10-40-30-40=80���ɴ���ͼ1�в�����ʾA�����μ��ɣ�����80��200��100%�ɵ�ϲ��A���˶�������ռ�İٷֱȣ���30��200��100%�ɵ�ϲ��D���˶�������ռ�İٷֱȣ������ðٷֱ�����ͼ2����Ӧ��λ�ü��ɣ�
��3����1200��20%�ɵ�ȫУϲ���������˶�������.
���������
��1����ͼ1�ɵ�ϲ����B���˶�������10�ˣ���ͼ2�ɵ�ϲ����B���˶�����ռ������5%��
����γ���������Ϊ��10��5%=200���ˣ���
��2������ͼ1��֪ϲ��B��C��D��E�����˶��������ֱ�Ϊ10��40��30��40�ˣ�
��ϲ��A���˶�������Ϊ��200-10-40-30-40=80��
��ϲ��A���˶�������ռ�İٷֱ�Ϊ��80��200��100%=40%��
ϲ��D���˶�������ռ�İٷֱ�Ϊ��30��200��100%=15%��
���������������ݲ���������ͼ�����£�
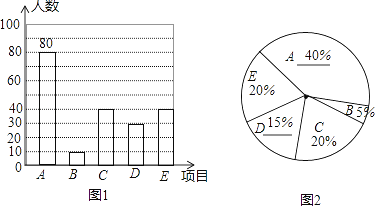
��3���ӳ��������п�֪��ϲ���������Լռ20%�����Թ���ȫУѧ����ϲ�������ѧ��Լռ20%������ԼΪ��1200��20%=240���ˣ�.
��ȫУѧ���У�ϲ�����������ԼΪ240�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
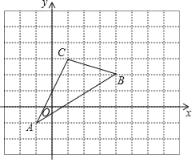
����Ŀ����ͼ��������ABC��ֱ������ϵ�У�
��1����ֱ��д����A��C��������꣺
��2��������ABC��������� ����
��3������������ABC����ƽ��1����λ��������ƽ��1����λ��������A��B��C����ͼ�л���������A��B��C������ʱ��B��������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����ù��������Ӽҳ������������е����![]() ��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����
��ͼ��ݻ��飮С��������ͬʱ�����İְ���ÿ����![]() ���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����
���ٶȴ�ͼ�����ͬһ����·���лؼң�С����ͼ���ͣ����![]() ���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����
���Ӻ���ԭ·��ԭ�ٷ��أ������dz�����![]() ���֣�ʱ��С�����֮��ľ���Ϊ
���֣�ʱ��С�����֮��ľ���Ϊ![]() ���ף���С���ְ����֮��ľ���Ϊ
���ף���С���ְ����֮��ľ���Ϊ![]() ���ף���ͼ������
���ף���ͼ������![]() ���߶�
���߶�![]() �ֱ��ʾ
�ֱ��ʾ![]() ��
��![]() ��
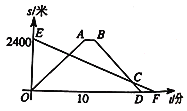
��![]() ֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
֮��ĺ�����ϵ��ͼ��С���Ӽҳ���������___�����ڷ���;���ϰְ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC�У���P��Q��BC���ϵ��������㣨�����B��C�غϣ�����AP��AQ��
��1����ͼ1����֪����BAP��20�㣬���AQB�Ķ�����
��2����Q����ֱ��AC�ĶԳƵ�ΪM���ֱ�����AM��PM��
�ٵ���P�ֱ��ڵ�Q�����Ҳ�ʱ���������⽫ͼ2��ͼ3��ȫ����д��������
��С����������IJ��룺��P��Q���˶��Ĺ����У�ʼ����PA��PM������С����֤�������������ȷ�ģ������ڢٵĵ�P��Q������λ�ù�ϵ��ѡ��һ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽Ѱ������������ֱ�����������߳�������ʱ���dz�֮Ϊ�������������������ж��٣��������й�����
��1������д�����鹴������
��2���Թ��카���������카��������ҪѰ��3����������ʹ������������������ƽ���ͣ������ڵ�������ƽ������������������ʽ��
���� ��2+�� ��2���� ��2������� ��2���� ��2���� ��2
��Ҫ�������Ϣ١��ڵ���ʽ�������ӳ˷���ʽ���֣������Ѿ�֪���ۣ�x+y��2����x��y��2��4xy�������ʽ���ұ�Ҳ��д���� ��2����ʽ�����ܷ��Ϣڵ���ʽ��
��˲�����x��m2��y��n2����m��nΪ������������m��n��������д����m��n����������������֤�������ǹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
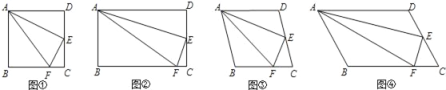
����Ŀ��С�����о������ε��й�����ʱ����������һ���⣺����ͼ�٣���������ABCD�У���E��CD���е㣬��F��BC���ϵ�һ�㣬�ҡ�FAE����EAD�����ܹ��ó�ʲô������ȷ�Ľ��ۣ���
��1��С�������о����֣�EF��AE�������С�������ֵĽ��ۼ���֤����
��2��С��֮���ּ�������������о�����������������Ϊ��������������������������ƽ���ı���������ͼ�ڡ�ͼ�ۡ�ͼ�ܣ����������������䣬��Ϊ��Ȼ����EF��AE������ͬ��С���Ĺ۵�������ͬ��С���Ĺ۵㣬��ȡͼ��Ϊ������֤�������㲻ͬ��С���Ĺ۵㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() �� ������
�� ������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
| �� |
|
| 0 | 1 | 2 | �� |
| �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵����ȷ���� ��
����������![]() ���һ������Ϊ
���һ������Ϊ![]() ��������������
��������������![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��
�������ߵĶԳ����ǣ�ֱ��![]() ������ ���ڶԳ������
������ ���ڶԳ������![]() ��
��![]() ���������.
���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�߶�AB��CD��ʾ���澵�ӣ���ֱ��AB��ֱ��CD������EF��������AB���䵽����CD������䵽����GH.���߷���ʱ����1=��2����3=��4�����н��ۣ���ֱ��EFƽ����ֱ��GH���ڡ�FGH�Ľ�ƽ�������ڵ�ֱ�ߴ�ֱ��ֱ��AB���ۡ�BFE�Ľ�ƽ�������ڵ�ֱ�ߴ�ֱ�ڡ�4�Ľ�ƽ�������ڵ�ֱ�ߣ��ܵ�CD�Ƶ�G˳ʱ����ת90ʱ��ֱ��EF��ֱ��GH��һ��ƽ�У�������ȷ���ǣ� ��

A. �٢ڢۢ�B. �٢ڢ�C. �ڢ�D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
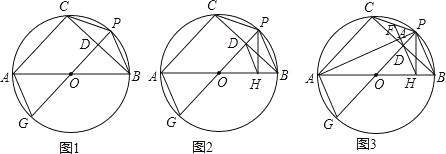
����Ŀ����O����ABC�����Բ��AB��ֱ������![]() ���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
��1����ͼ1����֤��AG=CP��
��2����ͼ2������P��AB�Ĵ��ߣ�����Ϊ��H������DH����֤��DH��AG��
��3����ͼ3������PA���ӳ�HD�ֱ���PA��PC�ཻ�ڵ�K��F����֪FK=2����ODH�����Ϊ2![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com