
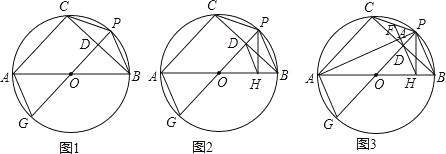
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
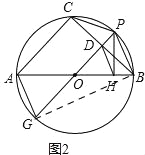
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
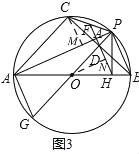
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
【答案】(1)证明见解析;
(2)证明见解析;
(3)AC=10
【解析】
试题分析:(1)利用等弧所对的圆周角相等即可求解;
(2)利用等弧所对的圆周角相等,得到角相等∠APG=∠CAP,判断出△BOD≌△POH,再得到角相等,从而判断出线平行;
(3)由三角形相似,得出比例式,△HON∽△CAM,![]() ,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
,再判断出四边形CDHM是平行四边形,最后经过计算即可求解.
试题解析:(1)∵过![]() 的中点P作⊙O的直径PG,
的中点P作⊙O的直径PG,
∴CP=PB,
∵AB,PG是相交的直径,
∴AG=PB,
∴AG=CP;
(2)证明:如图 2,连接BG
∵AB、PG都是⊙O的直径,
∴四边形AGBP是矩形,
∴AG∥PB,AG=PB,
∵P是弧BC的中点,
∴PC=BC=AG,
∴弧AG=弧CP,
∴∠APG=∠CAP,
∴AC∥PG,
∴PG⊥BC,
∵PH⊥AB,
∴∠BOD=90°=∠POH,
在△BOD和△POH中,
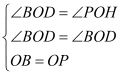 ,
,
∴△BOD≌△POH,
∴OD=OH,
∴∠ODH=![]() (180°﹣∠BOP)=∠OPB,
(180°﹣∠BOP)=∠OPB,
∴DH∥PB∥AG.
(3)如图3,作CM⊥AP于M,ON⊥DH于N,
∴∠HON=![]() ∠BOP=
∠BOP=![]() ∠COP=∠CAP,
∠COP=∠CAP,
∴△HON∽△CAM,
∴![]() ,
,
作PQ⊥AC于Q,
∴四边形CDPQ是矩形,
△APH与△APQ关于AP对称,
∴HQ⊥AP,
由(1)有:HK⊥AP,
∴点K在HQ上,
∴CK=PK,
∴PK是△CMP的中位线,
∴CM=2FK=4,MF=PF,
∵CM⊥AP,HK⊥AP,
∴CM∥HK,
∴∠BCM+∠CDH=180°,
∵∠BCM=∠CAP=∠BAP=∠PHK=∠MHK,
∴∠MHK+∠CDH=180°,
∴四边形CDHM是平行四边形,
∴DH=CM=4,DN=HN=2,
∵S△ODH=![]() DH×ON=
DH×ON=![]() ×4×ON=2
×4×ON=2![]() ,
,
∴ON=![]() ,
,
∴OH=![]() =5,
=5,
∴AC=![]() =10.
=10.


科目:初中数学 来源: 题型:
【题目】某网店销售某种商品,成本为30元/件,当销售价格为60元件/时,每天可售出100件,经市场调查发现,销售单价每降1元,每天销量增加10件.当销售单价为__________元时,每天获取的利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道 ![]() 是无理数,其整数部分是1,于是小明用
是无理数,其整数部分是1,于是小明用 ![]() ﹣1米表示
﹣1米表示 ![]() 的小数部分.请解答:
的小数部分.请解答:
(1)如果 ![]() 的小数部分为a,
的小数部分为a, ![]() +2的整数部分为b,求a+b﹣
+2的整数部分为b,求a+b﹣ ![]() 的值;
的值;
(2)已知10+ ![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB的两个端点坐标分别为A(a,1),B(﹣2,b),且满足 ![]() +
+ ![]() =0.
=0.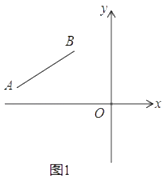
(1)则a= , b=;
(2)在y轴上是否存在点C,使三角形ABC的面积等于8?若存在,请求出点C的坐标;若不存在,请说明理由;
(3)如图2,将线段BA平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,求证:3n﹣2m=0.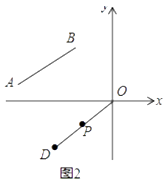
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班为了筹备演讲比赛,准备用200元钱购买日记本和钢笔两种奖品(两种都要买),其中日记本10元/本,钢笔l5元/支,在钱全部用完的条件下,购买的方案共有( )
A. 4种B. 5种C. 6种D. 7种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线经过坐标原点O,点A(6,﹣6![]() ),且以y轴为对称轴.
),且以y轴为对称轴.
(1)求抛物线的解析式;
(2)如图2,过点B(0,﹣![]() )作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;
)作x轴的平行线l,点C在直线l上,点D在y轴左侧的抛物线上,连接DB,以点D为圆心,以DB为半径画圆,⊙D与x轴相交于点M,N(点M在点N的左侧),连接CN,当MN=CN时,求锐角∠MNC的度数;
(3)如图3,在(2)的条件下,平移直线CN经过点A,与抛物线相交于另一点E,过点A作x轴的平行线m,过点(﹣3,0)作y轴的平行线n,直线m与直线n相交于点S,点R在直线n上,点P在EA的延长线上,连接SP,以SP为边向上作等边△SPQ,连接RQ,PR,若∠QRS=60°,线段PR的中点K恰好落在抛物线上,求Q点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com