
【题目】如图1,已知线段AB的两个端点坐标分别为A(a,1),B(﹣2,b),且满足 ![]() +
+ ![]() =0.
=0.
(1)则a= , b=;
(2)在y轴上是否存在点C,使三角形ABC的面积等于8?若存在,请求出点C的坐标;若不存在,请说明理由;
(3)如图2,将线段BA平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,求证:3n﹣2m=0.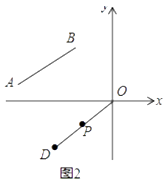
【答案】
(1)-5;3
(2)
存在,理由:如图1,
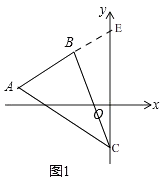
延长AB交y轴于E,
设C(0,c),
∵a=﹣5,b=3,
∴A(﹣5,1),B(﹣2,3),
∴AB的解析式为y= ![]() x+
x+ ![]() (﹣5≤x≤﹣2),
(﹣5≤x≤﹣2),
∴E(0, ![]() ),
),
∴CE=|c﹣ ![]() |,
|,
∵S△ABC=8,
∴S△ABC=S△ACE﹣S△BCE= ![]() CE|xA|﹣
CE|xA|﹣ ![]() CE|xB|=
CE|xB|= ![]() CE(|xA|﹣|xB|)=
CE(|xA|﹣|xB|)= ![]() ×|c﹣
×|c﹣ ![]() |×(5﹣2)=8,
|×(5﹣2)=8,
∴c= ![]() 或c=﹣
或c=﹣ ![]() ,
,
∴C(0, ![]() )或(0,﹣
)或(0,﹣ ![]() )
)
(3)
∵将线段BA平移得到线段OD,
∴OD的解析式为y= ![]() x(﹣3≤x≤0),
x(﹣3≤x≤0),
∵点P(m,n)在线段OD上,
∴n= ![]() m,
m,
∴3n﹣2n=0.
【解析】解:(1)∵ ![]() +
+ ![]() =0.
=0.
∴a+5=0,b﹣3=0,
∴a=﹣5,b=3,
故答案:﹣5,3;
【考点精析】关于本题考查的确定一次函数的表达式和三角形的面积,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处. 
(1)若∠PEF=48°,点F恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
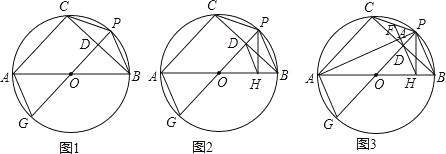
【题目】⊙O是△ABC的外接圆,AB是直径,过![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中的角平分线的性质与一个角的平分线性质相同.如题:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.请你结合条件认真研究,然后写出三个正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)2×(﹣3)3﹣4×(﹣3)+25
(2)﹣12﹣[2﹣(1+ ![]() ×0.5)]÷[32﹣(﹣2)2]
×0.5)]÷[32﹣(﹣2)2]
(3)4x2﹣3x+7﹣5x2+4x﹣5
(4)(3a2﹣ab+5)﹣(﹣4a2+2ab+5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com