
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处. 
(1)若∠PEF=48°,点F恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
【答案】
(1)解:①如图1,
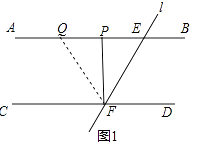
当点Q落在AB上,
∴FP⊥AB,
∴∠EFP=90°﹣∠PEF=42°,
②如图2,
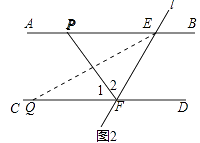
当点Q落在CD上,
∵将△EPF沿PF折叠,使顶点E落在点Q处,
∴PF垂直平分EQ,
∴∠1=∠2,
∵AB∥CD,
∴∠QFE=180°﹣∠PEF=132°,
∴∠PFE= ![]() QFE=66°
QFE=66°
(2)解:①如图3,

当点Q在平行线AB,CD之间时,
设∠PFQ=x,由折叠可得∠EFP=x,
∵∠CFQ= ![]() PFC,
PFC,
∴∠PFQ=∠CFQ=x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴75°+x+x+x=180°,
∴x=35°,
∴∠EFP=35°;
②如图4,

当点Q在CD的下方时,
设∠CFQ=x,由∠CFQ= ![]() PFC得,∠PFC=2x,
PFC得,∠PFC=2x,
∴∠PFQ=3x,
由折叠得,∠PFE=∠PFQ=3x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2x+3x+75°=180°,
∴x=21°,
∠EFP=3x=63°,
综上所述,∠EFP的度数是35°或63°
【解析】(1)①如图1,当点Q落在AB上,根据三角形的内角和即可得到结论;①如图2,当点Q落在CD上,由折叠的性质得到PF垂直平分EQ,得到∠1=∠2,根据平行线的性质即可得到结论;(2)①如图3,当点Q在平行线AB,CD之间时,设∠PFQ=x,由折叠可得∠EFP=x根据平行线的性质即可得到结论;②如图4,当点Q在CD的下方时,设∠CFQ=x,由∠CFQ= ![]() PFC得,∠PFC=2x根据平行线的性质即可得到结论.
PFC得,∠PFC=2x根据平行线的性质即可得到结论.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】在一个直角三角形中,两条直角边分别为![]() ,
, ![]() ,斜边为
,斜边为![]() :
:
(1)如果![]() ,
, ![]() ,则
,则![]() ,三角形的周长为 ,面积为 ;
,三角形的周长为 ,面积为 ;
(2)如果![]() ,
, ![]() ,则三角形的周长为 ,面积为 ;
,则三角形的周长为 ,面积为 ;
(3)如果![]() ,
, ![]() ,则
,则![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
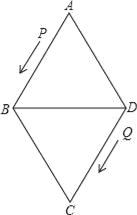
【题目】如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动.
(1)求BD的长;
(2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;
(3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某种商品,成本为30元/件,当销售价格为60元件/时,每天可售出100件,经市场调查发现,销售单价每降1元,每天销量增加10件.当销售单价为__________元时,每天获取的利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB的两个端点坐标分别为A(a,1),B(﹣2,b),且满足 ![]() +
+ ![]() =0.
=0.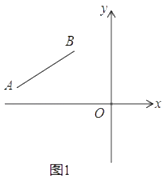
(1)则a= , b=;
(2)在y轴上是否存在点C,使三角形ABC的面积等于8?若存在,请求出点C的坐标;若不存在,请说明理由;
(3)如图2,将线段BA平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,求证:3n﹣2m=0.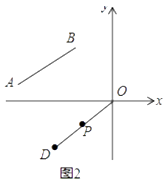
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com