
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.

【答案】证明见解析(2)60(3)30°
【解析】试题分析:(1)由等腰三角形的性质得出∠D=∠BCF,证出CF∥AD,由已知条件得出CG⊥CF,即可得出结论;
(2)①根据平行线的性质得出△BCF∽△BDA,得出![]() ,△BCF的面积:△BDA的面积=1:4,即可得出结果;
,△BCF的面积:△BDA的面积=1:4,即可得出结果;
②证出△BCF是等边三角形,得出∠B=60°,CF=BF=![]() AB,证出△ABD是等边三角形,CF=
AB,证出△ABD是等边三角形,CF=![]() AD,证出△AEF是等边三角形,得出AE=AF=
AD,证出△AEF是等边三角形,得出AE=AF=![]() AB=
AB=![]() AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
AD,因此CF=DE,证出四边形EFCD是平行四边形,即可得出结论.
试题解析:(1)∵AB=AD,FB=FC,
∴∠B=∠D,∠B=∠BCF,
∴∠D=∠BCF,
∴CF∥AD,
∵CG⊥AD,
∴CG⊥CF,
∴GC是⊙F的切线;
(2)解:①∵CF∥AD,
∴△BCF∽△BDA,
∴![]() =
=![]() ,△BCF的面积:△BDA的面积=1:4,
,△BCF的面积:△BDA的面积=1:4,
∴△BDA的面积=4△BCF的面积=4×15=60;
故答案为:60;
②当∠GCD的度数为30°时,四边形EFCD是菱形.理由如下:
∵CG⊥CF,∠GCD=30°,
∴∠FCB=60°,
∵FB=FC,
∴△BCF是等边三角形,
∴∠B=60°,CF=BF=![]() AB,
AB,
∵AB=AD,
∴△ABD是等边三角形,CF=![]() AD,
AD,
∴∠A=60°,
∵AF=EF,
∴△AEF是等边三角形,
∴AE=AF=![]() AB=
AB=![]() AD,
AD,
∴CF=DE,
又∵CF∥AD,
∴四边形EFCD是平行四边形,
∵CF=EF,
∴四边形EFCD是菱形;
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处. 
(1)若∠PEF=48°,点F恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
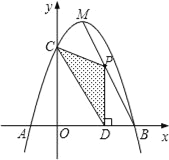
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中的角平分线的性质与一个角的平分线性质相同.如题:如图,△ABC中,AD是∠BAC的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为E,F.请你结合条件认真研究,然后写出三个正确的结论.
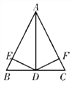
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com