
����Ŀ��ij�̵깺���ס��������ͺŵ���Ʒ��ÿ��������Ʒ�Ľ��۱�ÿ��������Ʒ�Ľ�����2Ԫ������80Ԫ����������Ʒ����������100Ԫ����������Ʒ��������ͬ.
��1����ס���������Ʒÿ���Ľ��۸�Ϊ����Ԫ��
��2��ÿ��������Ʒ�ۼ�Ϊ12Ԫ��ÿ��������Ʒ�ۼ�Ϊ15Ԫ���ó��б��ι���������Ʒ�������ȹ���������Ʒ��������3����5����Ҫʹ������Ʒȫ���۳�������������371Ԫ����ó��б������ٹ���������Ʒ���ټ���
���𰸡���1��8Ԫ��10Ԫ ��2��24��
��������
��1����ÿ��������Ʒ�Ľ���Ϊ![]() Ԫ����ÿ��������Ʒ�Ľ���Ϊ
Ԫ����ÿ��������Ʒ�Ľ���Ϊ![]() Ԫ�����������з��̣���⼴�ɣ�
Ԫ�����������з��̣���⼴�ɣ�
��2���蹺��������Ʒ![]() ������������Ʒ
������������Ʒ![]() ��������������������Ʒ�������ȹ���������Ʒ��������3����5�����������ס���������Ʒȫ���۳��ɻ�����371Ԫ���г�����ʽ�飬��˲���ʽ���ó�y��ȡֵ��Χ�������г���ͬ�ķ�����
��������������������Ʒ�������ȹ���������Ʒ��������3����5�����������ס���������Ʒȫ���۳��ɻ�����371Ԫ���г�����ʽ�飬��˲���ʽ���ó�y��ȡֵ��Χ�������г���ͬ�ķ�����
��1����ÿ��������Ʒ�Ľ���Ϊ![]() Ԫ����ÿ��������Ʒ�Ľ���Ϊ
Ԫ����ÿ��������Ʒ�Ľ���Ϊ![]() Ԫ
Ԫ
�������![]()
���![]()
������![]() �Ƿ�ʽ���̵Ľ�
�Ƿ�ʽ���̵Ľ�
![]()
��ÿ��������Ʒ�Ľ���Ϊ8Ԫ��ÿ��������Ʒ�Ľ���Ϊ10Ԫ.
��2���蹺��������Ʒ![]() ������������Ʒ
������������Ʒ![]() ����
����
�������![]()
���![]()
![]() ��������
��������
![]() ����СֵΪ24
����СֵΪ24
�𣺸��̵걾�����ٹ���������Ʒ24��.


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
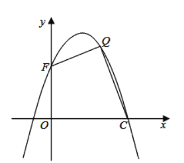
����Ŀ����ͼ��������y��ax2+bx+c��a��0���IJ���ͼ���䶥������Ϊ��1��m��������x�˵�һ�������ڵ㣨3��0���ͣ�4��0��֮�䣬�����н��ۣ���abc��0����a��b+c��0����b2��4a��c��m������һԪ���η���ax2+bx+c��m+1����������ȵ�ʵ������������ȷ���۵ĸ����ǣ�������

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��F�ֱ�Ϊ������ABCD�ı�AB��BC���е㣬AF��DE���ڵ�M�������н��ۣ��١�AME=90�㣻�ڡ�BAF=��EDB����MD=2AM=4EM����AM=![]() MF��������ȷ���۵ĸ����ǣ��� ��
MF��������ȷ���۵ĸ����ǣ��� ��
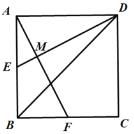
A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬�������߾�����
���㣬�������߾�����![]()

��1���������ߵĽ���ʽ��
��2����![]() ���������ϵ�һ�����㣨�����
���������ϵ�һ�����㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ʱ����
ʱ����![]() �����ꣻ
�����ꣻ
��3����ͼ��ʾ������������![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵĵ�һ�����ڣ��Ƿ����һ��
���������ߵĵ�һ�����ڣ��Ƿ����һ��![]() ��ʹ���ı���
��ʹ���ı���![]() �������������ڣ��������
�������������ڣ��������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�������ABCD�У�����P�ӵ�B������������B��C��D��B�˶������P������·��Ϊx����ABP�����Ϊy����y����x�ĺ�����������ͼ����ͼ����ʾ����ͼ���е�b���ڣ�������
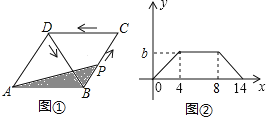
A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ����ABC�У�AB��4����D�DZ�AC��һ�㣬��AD��1����E��AB����һ�㣬����DE�����߶�DEΪֱ�DZ�������ֱ����DEF��D��E��F�������γ���ʱ�뷽������Fǡ������BC����ʱ����AE�ij���_____��
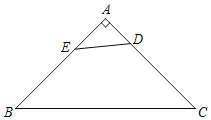
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
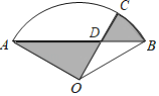
����Ŀ����ͼ��������![]() �У�
�У�![]() ���뾶
���뾶![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() ������Ӱ���ֵ����Ϊ________��
������Ӱ���ֵ����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
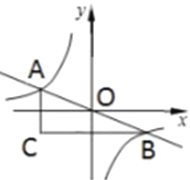
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ԭ���ֱ���뷴��������![]() ���ڵ�
���ڵ�![]() ���뷴��������
���뷴�������� ![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��Ĵ��ߣ�����
��Ĵ��ߣ�����![]() ��
��![]() ��Ĵ��ߣ���ֱ�߽��ڵ�
��Ĵ��ߣ���ֱ�߽��ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ֵΪ_______��
��ֵΪ_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com