
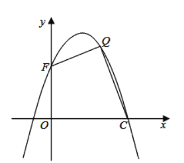
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 点坐标为(2,9)或(6,-7);(3)存在点Q(
点坐标为(2,9)或(6,-7);(3)存在点Q(![]() )使得四边形OFQC的面积最大,见解析.
)使得四边形OFQC的面积最大,见解析.
【解析】
(1)先由点![]() 在直线
在直线![]() 上求出点
上求出点![]() 的坐标,再利用待定系数法求解可得;
的坐标,再利用待定系数法求解可得;
(2)可设出![]() 点坐标,则可表示出
点坐标,则可表示出![]() 、
、![]() 的坐标,从而可表示出
的坐标,从而可表示出![]() 和
和![]() 的长,由条件可知到关于
的长,由条件可知到关于![]() 点坐标的方程,则可求得
点坐标的方程,则可求得![]() 点坐标;
点坐标;
(3)作![]() 轴于点
轴于点![]() ,设
,设![]() ,
,![]() ,知
,知![]() ,
,![]() ,
,![]() ,根据四边形
,根据四边形![]() 的面积
的面积![]() 建立关于
建立关于![]() 的函数,再利用二次函数的性质求解可得.
的函数,再利用二次函数的性质求解可得.
解:(1)![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,![]() ,
,
把![]() 、
、![]() 、
、![]() 三点坐标代入抛物线解析式可得
三点坐标代入抛物线解析式可得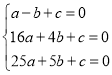 ,解得
,解得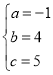 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
![]() ;
;
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,
时,![]() 与
与![]() 重合不合题意,舍去,
重合不合题意,舍去,
![]() ;
;
综上可知![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
(3)存在这样的点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
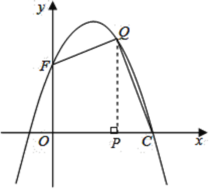
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
四边形![]() 的面积
的面积![]()
![]()
![]()
![]() ,
,
当![]() 时,四边形
时,四边形![]() 的面积取得最大值,最大值为
的面积取得最大值,最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE,设![]() ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )(提示:过点E、C、D作AB的垂线)
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )(提示:过点E、C、D作AB的垂线)

A.线段PDB.线段PCC.线段DED.线段PE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火车、运输工具可供选择,两种运输工具的主要参考数据如下:
运输工具 | 途中平均速度(单位:千米/时) | 途中平均费用(单位:元/千米) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中(含装卸时间)的损耗为150元/时,设运输路程为x(![]() )千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
)千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
(1)分别求出y1、y2与x的关系式;
(2)那么你认为采用哪种运输工具比较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ax2+bx+c开口向下,并且经过A(0,1)和M(2,-3)两点。
(1)若抛物线的对称轴为直线x= -1,求此抛物线的解析式;
(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;
(3)如果抛物线与x轴交于B、C两点,且∠BAC=90,求此时a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元,问公司租用的四座车和十一座车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校的社会实践活动中,一批学生协助搬运初一、二两个年级的图书,初一年级需要搬运的图书数量是初二年级需要搬运的图书数量的两倍.上午全部学生在初一年级搬运,下午一半的学生仍然留在初一年级(上下午的搬运时间相等)搬运,到放学时刚好把初一年级的图书搬运完.下午另一半的学生去初二年级搬运图书,到放学时还剩下一小部分未搬运,最后由三个学生再用一整天的时间刚好搬运完.如果这批学生每人每天搬运的效率是相同的,则这批学生共有人数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com