练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1，在等边△ABC中，点E、D分别是AC，BC边的中点，点P为AB边上的一个动点，连接PE，PD，PC，DE，设，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（ ）（提示：过点E、C、D作AB的垂线）

    A.线段PDB.线段PCC.线段DED.线段PE

    【答案】D

    【解析】

    先设等边三角形的边长为1个单位长度，再根据等边三角形的性质确定各线段取最小值时x的取值，再结合函数图像得到结论.

    设等边三角形的边长为1，则0≤x≤1，

    如图1，分别过点E,C,D作垂线，垂足分别为F,G,H，

    ∵点E、D分别是AC，BC边的中点，根据等边三角形的性质可得，

    当x=时，线段PE有最小值；

    当x=时，线段PC有最小值；

    当x=时，线段PD有最小值；

    又DE是△ABC的中位线为定值，

    由图2可知，当x=时,函数有最小值，故这条线段为PE，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DEF中，AB∥DE，点A，F，C，D在同一直线上，AF＝CD，∠AFE＝∠BCD．

    试说明：

    （1）△ABC≌△DEF；

    （2）BF∥EC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F

    （1）求证：EO=FO；

    （2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠A=90°，AD⊥BC，垂足为D.给出下列四个结论：①sinα=sinB；②sinβ=sinC；③sinB=cosC；④sinα=cosβ.其中正确的结论有_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰Rt△ABC中，∠C=90°，AC=4，矩形DEFG的顶点D、G分别在AC、BC上，边EF在AB上．

    （1）求证：△AED∽△DCG；

    （2）若矩形DEFG的面积为4，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

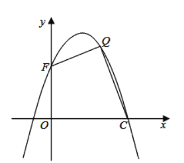
    【题目】如图，抛物线与直线相交于，两点，且抛物线经过点

    （1）求抛物线的解析式．

    （2）点是抛物线上的一个动点（不与点点重合），过点作直线轴于点，交直线于点．当时，求点坐标；

    （3）如图所示，设抛物线与轴交于点，在抛物线的第一象限内，是否存在一点，使得四边形的面积最大？若存在，请求出点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按要求完成下列推理证明．

    如图，已知点D为BC延长线上一点，CE∥AB．

    求证：∠A+∠B+∠ACB＝180°

    证明：∵CE∥AB，

    ∴∠1＝　 　，（　 　）

    ∠2＝　 　，（　 　）

    又∠1+∠2+∠ACB＝180°（平角的定义），

    ∴∠A+∠B+∠ACB＝180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m。

    （1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）

    （2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；

    （3）若球一定能越过球网，又不出边界，求h的取值范围。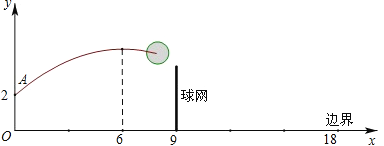

    查看答案和解析>>

    同步练习册答案