
【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE,设![]() ,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )(提示:过点E、C、D作AB的垂线)
,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )(提示:过点E、C、D作AB的垂线)

A.线段PDB.线段PCC.线段DED.线段PE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ax2+bx+c开口向下,并且经过A(0,1)和M(2,-3)两点。
(1)若抛物线的对称轴为直线x= -1,求此抛物线的解析式;
(2)如果抛物线的对称轴在y轴的左侧,试求a的取值范围;
(3)如果抛物线与x轴交于B、C两点,且∠BAC=90,求此时a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )
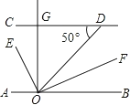
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元,问公司租用的四座车和十一座车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B,C两点,且D,E分别为顶点.则下列结论:

①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时y1>y2.
其中正确的结论是( )
A. ①③④ B. ①③ C. ①②④ D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com