Question

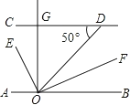
【题目】如图，CD∥AB，OE平分∠AOD，OF⊥OE，OG⊥CD，∠CDO＝50°，则下列结论：① ∠AOE＝65°；② OF平分∠BOD；③ ∠GOE＝∠DOF；④ ∠AOE＝∠GOD，其中正确结论的个数是（ ）

A. 1个B. 2个C. 3个D. 4个

Answer 1

【答案】C

【解析】

由CD∥AB，根据两直线平行，内错角相等，即可求得∠BOD的度数，∠AOE的度数；又由OF⊥OE，即可求得∠BOF的度数，得到OF平分∠BOD；又由OG⊥CD，即可求得∠GOE与∠DOF的度数．

∵CD∥AB，

∴∠BOD=∠CDO=50°，

∴∠AOD=180°-∠BOD=130°，

∵OE平分∠AOD，

∴∠AOE=∠AOD=65°；

故①正确；

∵OF⊥OE，

∴∠BOF=90°-∠AOE=25°，

∵∠BOD=50°，

∴OF平分∠BOD；

故②正确；

∵OG⊥CD，CD∥AB，

∴OG⊥AB，

∴∠GOE=90°-∠AOE=25°，

∵∠DOF=∠BOD=25°，

∴∠GOE=∠DOF；

故③正确；

∴∠AOE=65°，∠GOD=40°；

故④错误．

故选C．