练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，五边形ABCDE中，∠A＝140°，∠B＝120°，∠E＝90°，CP和DP分别是∠BCD、∠EDC的外角平分线，且相交于点P，则∠CPD＝__________°．

    【答案】95

    【解析】

    根据多边形的内角和定理：（n-2）180°，可得出∠BCD、∠EDC的和，从而得出相邻两外角和，然后根据角平分线及三角形内角和定理即可得出答案．

    解：五边形ABCDE的内角和为：（5-2）×180°=540°，
    ∴∠BCD+∠EDC=540°-140°-120°-90°=190°，
    又∵CP和DP分别是∠BCD、∠EDC的外角平分线，
    ∴∠PCD+∠PDC=（360°-∠BCD-∠EDC）=85°，
    根据三角形内角和定理得：∠CPD=180°-85°=95°．
    故答案为：95．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；

    ③3a+c=0；④当y＞0时，x的取值范围是﹣1≤x＜3；⑤当x＜0时，y随x增大而增大，其中结论正确的是_____（只需填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0)，且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD∥AB，OE平分∠AOD，OF⊥OE，OG⊥CD，∠CDO＝50°，则下列结论：① ∠AOE＝65°；② OF平分∠BOD；③ ∠GOE＝∠DOF；④ ∠AOE＝∠GOD，其中正确结论的个数是（ ）

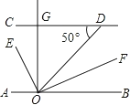
    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】黄冈某地“杜鹃节”期间，某公司70名职工组团前往参观欣赏，旅游景点规定：①门票每人60元，无优惠；②上山游玩可坐景点观光车，观光车有四座和十一座车，四座车每辆60元，十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元，问公司租用的四座车和十一座车各多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A、B的坐标分别是（0，2）、（4，0），点P是直线y=2x+2上的一动点，当以P为圆心，PO为半径的圆与△AOB的一条边所在直线相切时，点P的坐标为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y1=(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1，3)，过点A作x轴的平行线，分别交两条抛物线于B，C两点，且D，E分别为顶点.则下列结论：

    ①a=；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时y1＞y2.

    其中正确的结论是(　　)

    A. ①③④ B. ①③ C. ①②④ D. ②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，以点为圆心，以为半径的圆与轴相交于点，与轴相交于点．

    （1）若抛物线经过两点，求抛物线的解析式，并判断点是否在该抛物线上．

    （2）在（1）中的抛物线的对称轴上求一点，使得的周长最小．

    （3）设为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点，使得四边形是平行四边形．若存在，求出点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一个长方形放置在平面直角坐标系中，，点是的中点，反比例函数图像过点且和相交于点.

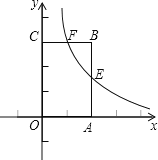
    （1）求直线和反比例函数的解析式；

    （2）求四边形的面积.

    查看答案和解析>>

    同步练习册答案