
【题目】抛物线y=ax2+bx+c(a<0)经过点(-1,0),且满足4a+2b+c>0.以下结论(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
(1)把点(-1,0)代入解析式可得ab+c=0①,结合4a+2b+c>0②,即可整理出a+b>0;
(2)由②+①×2得,6a+3c>0,结合a<0,故可求出a+c>0;
(3)画草图可知c>0,结合a-b+c=0,可整理得-a+b+c=2c>0,从而求得-a+b+c>0;
(4)由ab+c=0可得,b22ac5a2=(c+2a)(c2a),由(2)可知2a+c>0,再由a<0, c>0可知c-2a>0,故可得出(c+2a)(c-2a)>0,即b2-2ac-5a2>0,进而可得出结论.
(1) ∵抛物线y=ax2+bx+c(a<0)经过点(1,0),
∴原式可化为ab+c=0①,
又∵4a+2b+c>0②,
∴②①得:
3a+3b>0,
即a+b>0,
故正确;
(2)②+①×2得,
6a+3c>0,
即2a+c>0,
∴a+c>a,
∵a<0,
∴a>0,
∴a+c>0;
故正确;
(3)因为4a+2b+c>0,可以看作y=ax2+bx+c(a<0)当x=2时的值大于0,草图为:
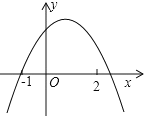
可见c>0,
∵ab+c=0,
∴a+bc=0,
两边同时加2c得a+bc+2c=2c,
整理得a+b+c=2c>0,
即a+b+c>0;
故正确;
(4)∵过(1,0),代入得ab+c=0,
∴b22ac5a2=(a+c)22ac5a2=c24a2=(c+2a)(c2a)
由(2)可知2a+c>0,
由(3)可知c>0,
∵a<0,
∴c2a>0②
∴(c+2a)(c2a)>0,
∴b22ac5a2>0,
即b22ac>5a2,
故正确.
∴正确的个数有4个.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,AB=2,∠DAB=60°,点 E 是 AD 边的中点,点 M 是 AB 边上的一个动点(不与点 A 重合), 延长 ME 交 CD 的延长线于点 N,连接MD,AN.

(1)求证:四边形 AMDN 是平行四边形.
(2)当 AM 的值为何值时,四边形 AMDN 是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()

(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
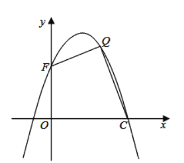
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法正确的个数有( )
①若 m>n,则![]() ;②由三条线段首尾顺次相接所组成的图形叫做三角形;③有两个角互余的三角形一定是直角三角形;④各边都相等的多边形是正多边形;⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
;②由三条线段首尾顺次相接所组成的图形叫做三角形;③有两个角互余的三角形一定是直角三角形;④各边都相等的多边形是正多边形;⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中,∠A=140°,∠B=120°,∠E=90°,CP和DP分别是∠BCD、∠EDC的外角平分线,且相交于点P,则∠CPD=__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
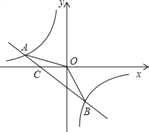
【题目】如图,已知A(–4,n),B(2,–4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com