
����Ŀ������һˮ�����۹�˾���轫һ����������ij�أ��������������乤�߿ɹ�ѡ���������乤�ߵ���Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶȣ���λ��ǧ��/ʱ�� | ;��ƽ�����ã���λ��Ԫ/ǧ�ף� | װжʱ�䣨��λ��Сʱ�� | װж���ã���λ��Ԫ�� |
���� | 75 | 8 | 2 | 1000 |
�� | 100 | 6 | 4 | 2000 |
������ˮ������������У���װжʱ�䣩�����Ϊ150Ԫ/ʱ��������·��Ϊx��![]() ��ǧ�ף����������������ܷ���Ϊy1Ԫ���û����������ܷ���Ϊy2Ԫ.
��ǧ�ף����������������ܷ���Ϊy1Ԫ���û����������ܷ���Ϊy2Ԫ.
��1���ֱ����y1��y2��x�Ĺ�ϵʽ��
��2����ô����Ϊ�����������乤�߱ȽϺã�
���𰸡���1��![]() ��
��![]() ����2��������·�̴���520ǧ��ʱ�����û�����Ϻã�������·�̵���520ǧ��ʱ���������乤��һ����������·��С��520ǧ��ʱ��������������Ϻã�
����2��������·�̴���520ǧ��ʱ�����û�����Ϻã�������·�̵���520ǧ��ʱ���������乤��һ����������·��С��520ǧ��ʱ��������������Ϻã�
��������
��1�����ݱ������Ϣ��ϵ�����ϵ����д����ϵʽ��
��2�����������г�����ʽ���ʽ������⣬����x��ȡֵ�жϷ������ٵ����.
�⣺��1��������·��Ϊx��![]() ��ǧ�ף����������������ܷ���Ϊy1Ԫ��
��ǧ�ף����������������ܷ���Ϊy1Ԫ��
�û����������ܷ���Ϊy2Ԫ�����������
![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
��2����![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��
��![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��
��![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��
��������·�̴���520ǧ��ʱ�����û�����Ϻã�
������·�̵���520ǧ��ʱ���������乤��һ����
������·��С��520ǧ��ʱ��������������Ϻã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ xOy �У����� ABOC �Ķ��� O ������ԭ�㣬�� BO �� x ��ĸ������ϣ����� C������Ϊ����3��4�������������� y ![]() ��ͼ�������ζԽ��� AO ���� D �㣬���� BD���� BD��x ��ʱ��k��ֵ�ǣ� ��
��ͼ�������ζԽ��� AO ���� D �㣬���� BD���� BD��x ��ʱ��k��ֵ�ǣ� ��

A.![]() B.
B.![]() C.��12D.
C.��12D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC��D��AEƽ�֡�BAC��
��1������B��30�㣬��C��70�㣬���DAE���� ��
��2������C����B��30�㣬���DAE���� ����
��3������C����B��������C����B�������DAE�Ķ������ú����Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=4������DEFG�Ķ���D��G�ֱ���AC��BC�ϣ���EF��AB�ϣ�
��1����֤����AED�ס�DCG��
��2��������DEFG�����Ϊ4����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪MB=ND����MBA=��NDC�������ĸ����������ж���ABM�ա�CDN�� ��

A.AM=CNB.AB=CD C.AM��CN D.��M=��N
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
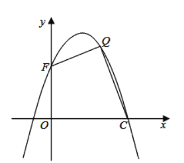
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬�������߾�����
���㣬�������߾�����![]()

��1���������ߵĽ���ʽ��
��2����![]() ���������ϵ�һ�����㣨�����
���������ϵ�һ�����㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ʱ����
ʱ����![]() �����ꣻ
�����ꣻ
��3����ͼ��ʾ������������![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵĵ�һ�����ڣ��Ƿ����һ��
���������ߵĵ�һ�����ڣ��Ƿ����һ��![]() ��ʹ���ı���
��ʹ���ı���![]() �������������ڣ��������
�������������ڣ��������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ xoy �У���֪�� A ������Ϊ��-2��0����
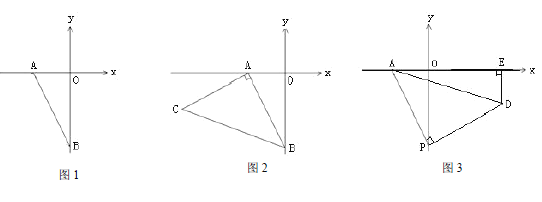
��1����ͼ 1������ B ������Ϊ��0��-4��ʱ������AOB ������� ��
��2����ͼ 2���ڣ�1���������£����� A �� AC��AB����ʹ AC=AB������������ڵĵ� C �����ꣻ
��3����ͼ 3��P Ϊ y �Ḻ������һ�㣬���� P �� PD��PA����ʹ PD=PA�������������ڵĵ� D �� DE��x ���� E�����ж� OP-DE ��ֵ�Ƿ����仯�����������仯��������ֵ���������仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
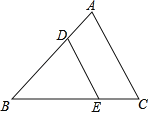
����Ŀ����ͼ����֪��D��E�ֱ�ΪAB��BC�ϵĵ㣬����DE����A��70�㣬��ADE��110�㣮
��1����֤����C����BED��
��2����ͼ����D����DF��BC������ΪF������AE������EDF����EAC��28�㣬���C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����ABK�Ľ�ƽ����BE�ķ����ӳ��ߺ���DCK�Ľ�ƽ����CF�ķ����ӳ��߽��ڵ�H����K����H=27��������K=��������

A. 76�� B. 78�� C. 80�� D. 82��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com