
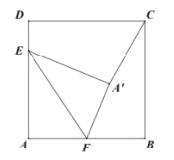
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 为
为![]() 的靠近点
的靠近点![]() 的四等分点,点
的四等分点,点![]() 为
为![]() 的中点, 将
的中点, 将![]() 沿着
沿着![]() 翻折得
翻折得![]() ,连接
,连接![]() ,则点
,则点![]() 到
到![]() 的距离为( )
的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点A'作GH∥AD,交AB、CD于点G、H,过点E作EK⊥GH,垂足为点K,先通过折叠可得A'E= AE=3,A'F= AF=2,∠A'=∠A=90°,再结合∠EKG=∠G=90°,证得△A'KE∽△FGA',根据相似三角形的性质可得相似比为3:2,故可设A'K=3x, FG=2x,进而表示出EK和A'G的长,再根据相似比列出方程求出x,即可求得A'G、A'H的长,再用勾股定理求得A'C的长,最后根据等积法求得点D到![]() 的距离即可.
的距离即可.
解:如图,过点A'作GH∥AD,交AB、CD于点G、H,过点E作EK⊥GH,垂足为点K,
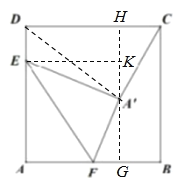
则四边形AGKE、DEKH、BGHC均为矩形,
由题意可知DE=1,AE=3,AF=BF=2,DC=4,∠A=90°,
∵折叠,
∴A'E= AE=3,A'F= AF=2,∠A'=∠A=90°,
又∵∠EKG=∠G=90°,
∴△A'KE∽△FGA',
∴![]() ,
,
设A'K=3x,则FG=2x,
在矩形AGKE中,AE=KG=3,EK=AG=2+2x,
∴A'G=KG- A'K=3-3x
∴![]()
解得x=![]() ,
,
∴A'H=HG- A'G=4-(3-3×![]() )=
)=![]() ,
,
又∵HC=CD-DK=4-(2+2×![]() )=
)=![]() ,
,
∴在Rt△A'HC中,A'C=![]() ,
,
设点D到A'C的距离为h,
则S△A'DC=![]() A'C×h=
A'C×h=![]() CD×A'H,
CD×A'H,
∴A'C×h=CD×A'H,
∴![]() ,
,
解得h=![]() ,
,
故选:C.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
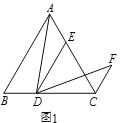
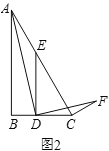
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
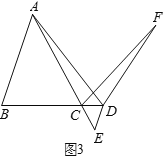
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数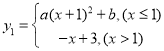 (
(![]() 为常数且
为常数且![]() ),已知当
),已知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,请对该函数及其图像进行如下探究:
,请对该函数及其图像进行如下探究:

(1)求函数![]() 的解析式;
的解析式;
(2)如图,请在平面直角坐标系中,画出该函数的图像;
(3)结合所画函数图像,请写出该函数的一条性质;
(4)解决问题:若函数![]() 与
与![]() 至少有两个公共点,请直接写出
至少有两个公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
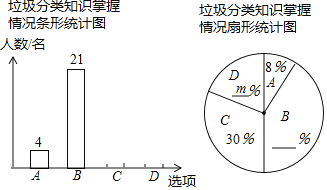
【题目】为响应市政府关于“垃圾不落地![]() 市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解
市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解![]() ”四种,并将调查结果绘制成以下两幅不完整的统计图
”四种,并将调查结果绘制成以下两幅不完整的统计图![]() 请根据图中提供的信息,解答下列问题;
请根据图中提供的信息,解答下列问题;
![]() 求
求![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
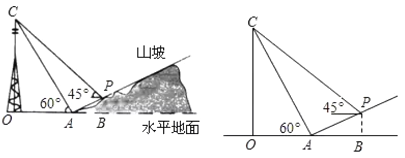
【题目】如图,某人在山坡坡脚![]() 处测得电视塔尖点
处测得电视塔尖点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得点
处再测得点![]() 的仰角为
的仰角为![]() ,已知
,已知![]() 米,山坡坡度
米,山坡坡度![]() ,且
,且![]() 在同一条直线上,其中测倾器高度忽略不计.
在同一条直线上,其中测倾器高度忽略不计.
(1)求电视塔![]() 的高度;(计算结果保留根号形式)
的高度;(计算结果保留根号形式)
(2)求此人所在位置点![]() 的铅直高度.(结果精确到0.1米,参考数据:
的铅直高度.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
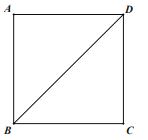
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com