练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

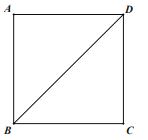
    【题目】在正方形ABCD中，E是CD边上的点，过点E作EF⊥BD于F．

    (1)尺规作图：在图中求作点E，使得EF=EC；(保留作图痕迹，不写作法)

    (2)在(1)的条件下，连接FC，求∠BCF的度数．

    【答案】（1）作图见解析；（2）∠BCF=67.5°.

    【解析】

    （1）作∠CBD的角平分线即可．

    （2）证明BF＝BC，利用等腰三角形的性质即可解决问题．

    解：（1）如图，点E即为所求．

    （2）∵四边形ABCD是正方形，

    ∴∠BCD＝90°，BC＝CD．

    ∴∠DBC＝∠CDB＝45°，

    ∵EF⊥BD，

    ∴∠BFE＝90°．

    由（1）得EF＝EC，BE＝BE，

    ∴Rt△BFE≌Rt△BCE（HL）

    ∴BC＝BF．

    ∴∠BCF＝∠BFC，

    ∴∠BCF＝(180°∠FBC)＝67.5°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为的正方形中，点为的靠近点的四等分点，点为的中点， 将沿着翻折得，连接，则点到的距离为（ 　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点A（x1，y1），B（x2，y2），若x1x2+y1y2＝0，且A，B均不为原点，则称A和B互为正交点．比如：A（1，1），B（2，﹣2），其中1×2+1×（﹣2）＝0，那么A和B互为正交点．

    （1）点P和Q互为正交点，P的坐标为（﹣2，3），

    ①如果Q的坐标为（6，m），那么m的值为多少；

    ②如果Q的坐标为（x，y），求y与x之间的关系式；

    （2）点M和N互为正交点，直接写出∠MON的度数；

    （3）点C，D是以（0，2）为圆心，半径为2的圆上的正交点，以线段CD为边，构造正方形CDEF，圆心F在正方形CDEF的外部，求线段OE长度的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．即：如图1，在Rt△ABC中，∠ACB=90°，∠ABC=30°，则：AC=AB．

    探究结论：小明同学对以上结论作了进一步研究．

    （1）如图1，连接AB边上中线CE，由于CE=AB，易得结论：①△ACE为等边三角形；②BE与CE之间的数量关系为　　．

    （2）如图2，点D是边CB上任意一点，连接AD，作等边△ADE，且点E在∠ACB的内部，连接BE．试探究线段BE与DE之间的数量关系，写出你的猜想并加以证明．

    （3）当点D为边CB延长线上任意一点时，在（2）条件的基础上，线段BE与DE之间存在怎样的数量关系？请直接写出你的结论　　．

    拓展应用：如图3，在平面直角坐标系xOy中，点A的坐标为（﹣，1），点B是x轴正半轴上的一动点，以AB为边作等边△ABC，当C点在第一象限内，且B（2，0）时，求C点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

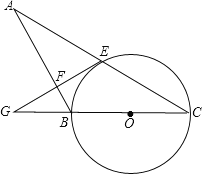
    【题目】如图，AB＝BC，以BC为直径作⊙O，AC交⊙O于点E，过点E作EG⊥AB于点F，交CB的延长线于点G．

    （1）求证：EG是⊙O的切线；

    （2）若GF＝2，GB＝4，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在国家大数据战略的引领下，我国在人工智能领域取得显著成就，自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军，这得益于所建立的大数据中心的规模和数据存储量，它们决定着人工智能深度学习的质量和速度，其中的一个大数据中心能存储580亿本书籍，将580亿用科学记数法表示应为（ ）．

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，抛物线G：y＝mx2+2mx+m﹣1（m≠0）与y轴交于点C，抛物线G的顶点为D，直线：y＝mx+m﹣1（m≠0）．

    （1）当m＝1时，画出直线和抛物线G，并直接写出直线被抛物线G截得的线段长．

    （2）随着m取值的变化，判断点C，D是否都在直线上并说明理由．

    （3）若直线被抛物线G截得的线段长不小于2，结合函数的图象，直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y＝ax﹣a与y＝（a≠0）在同一直角坐标系中的图象可能是（　　）

    A.B.

    C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校组织了一次体育测试，测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”．规定：每名学生测试三项，其中A、B为必测项目，第三项在C、D、E中随机抽取，每项10分（成绩均为整数且不低于0分）．

    （1）完成A、B必测项目后，用列表法，求甲、乙两同学第三项抽取不同项目的概率；

    （2）某班有6名男生抽到了E“800米跑”项目，他们的成绩分别（单位：分）为：x，6，7，8，8，9．

    ①已知这组成绩的平均数和中位数相等，且x不是这组成绩中最高的，则x= ；

    ②该班学生丙因病错过了测试，补测抽到了E“800米跑”项目，加上丙同学的成绩后，发现这组成绩的众数与中位数相等，但平均数比原来的平均数小，则丙同学“800米跑”的成绩为多少？；

    甲

    乙

    查看答案和解析>>

    同步练习册答案