
����Ŀ����ƽ��ֱ������ϵxOy�У�������G��y��mx2+2mx+m��1��m��0����y�ύ�ڵ�C��������G�Ķ���ΪD��ֱ�ߣ�y��mx+m��1��m��0����

��1����m��1ʱ������ֱ�ߺ�������G����ֱ��д��ֱ�߱�������G�صõ��߶γ���
��2������mȡֵ�ı仯���жϵ�C��D�Ƿ���ֱ���ϲ�˵�����ɣ�
��3����ֱ�߱�������G�صõ��߶γ���С��2����Ϻ�����ͼ��ֱ��д��m��ȡֵ��Χ��
���𰸡���1������������2������mȡ��ֵ����C��D����ֱ���ϣ�����������3��m��ȡֵ��Χ��m�ܩ�![]() ��m��
��m��![]() ��
��
��������
��1����m��1ʱ��������G�ĺ�������ʽΪy��x2+2x��ֱ�ߵĺ�������ʽΪy��x�����ֱ�߱�������G�صõ��߶Σ��ٻ�������������ͼ�ɣ�
��2�������C��D��������꣬�ٴ���ֱ�ߵĽ���ʽ���м��鼴�ɣ�
��3��������ֱ���������ߵĽ���ʽ��������ǵĽ������꣬�ٸ�������������֮��ľ��벻С��2�г�����ʽ����⼴�ɣ�
��1����m=1ʱ��������G�ĺ�������ʽΪy=x2+2x��ֱ�ߵĺ�������ʽΪy=x��
ֱ�߱�������G�صõ��߶γ�Ϊ![]() ��
��
����������������ͼ����ͼ��ʾ��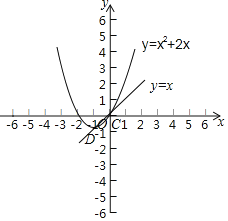
��2������mȡ��ֵ����C��D����ֱ���ϣ��������£�
��������G��y=mx2+2mx+m-1��m��0����y�ύ�ڵ�C��
���C������ΪC��0��m-1����
��y=mx2+2mx+m-1=m��x+1��2-1��
��������G�Ķ���D������Ϊ��-1��-1����
����ֱ�ߣ�y=mx+m-1��m��0����
��x=0ʱ��y=m-1��
��x=-1ʱ��y=m����-1��+m-1=-1��
������mȡ��ֵ����C��D����ֱ���ϣ�
��3���ⷽ����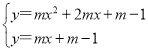 ��
��
��![]() ����
����![]() ��
��
��ֱ����������G�Ľ���Ϊ��0��m-1������-1��-1����
��ֱ�߱�������G�صõ��߶γ���С��2��
��![]() ��2��
��2��
��1+m2��4��m2��3��
��m��-![]() ��m��
��m��![]()
��
��m��ȡֵ��Χ��m��-![]() ��m��
��m��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
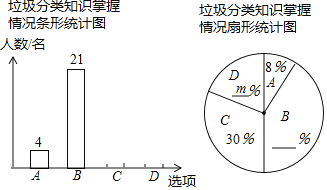
����Ŀ��Ϊ��Ӧ���������ڡ����������![]() �������������������������֣���������ѧ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣻B���Ƚ��˽⣻C���˽���٣�D�����˽�
�������������������������֣���������ѧ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣻B���Ƚ��˽⣻C���˽���٣�D�����˽�![]() �����֣��������������Ƴ�����������������ͳ��ͼ
�����֣��������������Ƴ�����������������ͳ��ͼ![]() �����ͼ���ṩ����Ϣ������������⣻
�����ͼ���ṩ����Ϣ������������⣻
![]() ��
��![]() ______������ȫ����ͳ��ͼ��
______������ȫ����ͳ��ͼ��
![]() ����Уѧ������Ϊ1000�������ݵ����������Ƹ�У���dz��˽⡱�롰�Ƚ��˽⡱��ѧ������______����
����Уѧ������Ϊ1000�������ݵ����������Ƹ�У���dz��˽⡱�롰�Ƚ��˽⡱��ѧ������______����
![]() ��֪���dz��˽⡱����3��������1��Ů�������������ȡ2����ȫУ�����������֪ʶ�������뻭��״ͼ���б��ķ�������ǡ�ó鵽1��1Ů�ĸ��ʣ�
��֪���dz��˽⡱����3��������1��Ů�������������ȡ2����ȫУ�����������֪ʶ�������뻭��״ͼ���б��ķ�������ǡ�ó鵽1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ�����ﴫͳ�Ļ����ĺ��٣�ijѧУ����ȫУ1200��ѧ�����о���ʫ���б�������ڻ֮��ٰ쾭��ʫ�ʴ�����Ϊ�˽Ȿ��ϵ�л�ij���Ч����ѧУ��ί�ڻ����֮���������ȡ����ѧ��������һ��ʫ���б��������������������Ƴɵ�ͳ��ͼ�����֣���ͼ��ʾ��
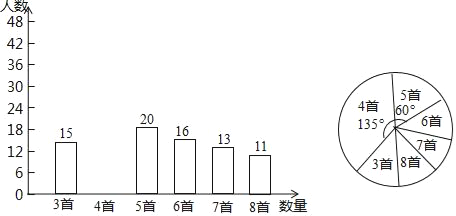
����������һ���£��ٴγ���ⲿ��ѧ����һ��ʫ���б������������Ƴ�ͳ�Ʊ�
һ��ʫ���б����� | 3�� | 4�� | 5�� | 6�� | 7�� | 8�� |
���� | 10 | 10 | 15 | 40 | 25 | 20 |
����ݵ������Ϣ
��1�������֮��ѧ����һ��ʫ���б�����������λ��Ϊ������
��2�����ƴ�����һ���¸�Уѧ��һ��ʫ���б�6�ף���6�ף����ϵ�������
��3��ѡ���ʵ���ͳ��������������ͬ�ĽǶȷ������ε����������ݣ����۸�У����ʫ���б�ϵ�л��Ч����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
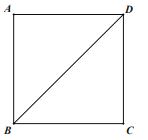
����Ŀ����������ABCD�У�E��CD���ϵĵ㣬����E��EF��BD��F��
(1)�߹���ͼ����ͼ��������E��ʹ��EF=EC��(������ͼ�ۼ�����д����)
(2)��(1)�������£�����FC�����BCF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�����ʦ��ͬѧ�ǶԸ�����������![]() ���������ʵ�ƽ��ֱ������ϵ������ʾ������������꣮������4��ͬѧ��ʾ����������Ľ����
���������ʵ�ƽ��ֱ������ϵ������ʾ������������꣮������4��ͬѧ��ʾ����������Ľ����
��ͬѧ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��ͬѧ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��ͬѧ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��ͬѧ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������ͬѧ��ʾ�Ľ���У��ĸ�������궼��ʾ��ȷ��ͬѧ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AD��б���ϵ����ߣ�E��AD���е㣬����A��AF��BC��BE���ӳ�����F������CF��
��1����֤��BD=AF��
��2���ж��ı���ADCF����״����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
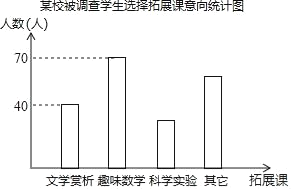
����Ŀ��Ϊ�ḻѧ���Ŀ������ijУ�ǻ���չ������չ�λ���ֱ��ǡ���ѧ����������Ȥζ��ѧ��������ѧʵ�顱����Ŀ��Ҫ��ÿλѧ������ѡ������һ����չ�βμӣ������ȡ��У����β���ѧ������ѡ����չ�ε�������е��ˣ�������Ľ������������ͳ��ͼ�Ͳ�������ͳ�Ʊ���
ijУ������ѧ��ѡ����չ������ͳ�Ʊ�
ѡ������ | ��ռ�ٷֱ� |
��ѧ���� | �� �� |
Ȥζ��ѧ | 35% |
��ѧʵ�� | �� �� |
���� | 30% |
��1����У��2000��ѧ����������ƴ�Լ�ж�����ѧ���μӿ�ѧʵ����չ�Σ�����ȫͳ�Ʊ���
��2����У�μӿ�ѧʵ����չ�ε�ѧ������ֳ�A��B��C����������ͬ�İ༶��С�ۺ�С�����μӿ�ѧʵ����չ�Σ�������ͬ�༶�ĸ��ʣ�����״ͼ���б�����⣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����Լ��ĩ��ѩ�����Ժ���ݳ������ǵļҷֱ�����Ժ1200m��2000m�����˷ֱ�Ӽ���ͬʱ��������֪С����С�յ��ٶȱ���3��4�����С����С����ǰ4min�����Ժ�������˵��ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������ƽ���߽���һ�㣬������Ϊ�����ε�����(������������Բ��Բ��) . ���ڹ涨������ı��ε�������ƽ���߽���һ�㣬���ǰ�������Ϊ���ı��ε����ġ���
�������
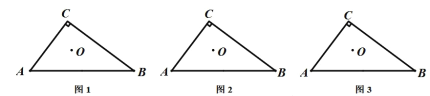
��1����ͼ1������ABC�У���C=90������OΪ��ABC�����ģ���ֱ��DE�ֱ�AC��BC�ڵ�D��E���ҵ�O��ȻΪ�ı���ABED�����ģ�������ֱ��DE���Ի�������?����ͼ1�л���һ������������ֱ��DE������Ҫ˵��������
����̽��
��2����ͼ2������ABC�У���C=90���� AC=3�� BC=4��������(1)��������һ��ֱ��DE // AB�����ʱ�߶�DE�ij���
������
��3����ͼ3������ABC�У���C=90���� AC=3��BC=4�������㣨1�����������߶�DE�Ƿ������Сֵ?������ڣ���������ֵ;��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com