
【题目】为丰富学生的课余生活,某校记划开展三种拓展课活动,分别是“文学赏析”,“趣味数学”,“科学实验”等项目,要求每位学生自主选择其中一项拓展课参加.随机抽取该校各年段部分学生,对选择拓展课的意向进行调査,将调查的结果制作成以下统计图和不完整的统计表.
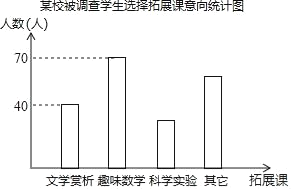
某校被调查学生选择拓展课意向统计表
选择意向 | 所占百分比 |
文学赏析 |
|
趣味数学 | 35% |
科学实验 |
|
其它 | 30% |
(1)该校有2000名学生,请你估计大约有多少名学生参加科学实验拓展课,并补全统计表.
(2)该校参加科学实验拓展课的学生随机分成A,B,C三个人数相同的班级.小慧和小明都参加科学实验拓展课,求他们同班级的概率(画树状图或列表法求解)
【答案】(1)300人,15%,20%;(2)![]()
【解析】
(1)先根据趣味数学的人数和百分比求得总人数,再依次求出其它和科学实验的人数,从而进一步计算可得;
(2)画树状图展示所有9种等可能性情况,找出两个人在一个班的结果数,然后根据概率公式求解.
(1)∵被调查的学生人数为70÷35%=200(人),
∴其它类的人数为200×30%=60(人),
∴科学实验的人数为200﹣(40+70+60)=30(人),
则文学赏析对应的百分比为![]() 100%=20%,科学实验对应的百分比为
100%=20%,科学实验对应的百分比为![]() 100%=15%;全校参加科学实验拓展课的人数=2000×15%=300(人)
100%=15%;全校参加科学实验拓展课的人数=2000×15%=300(人)
故表格依次填写:15%,20%.

(2)画树状图为:
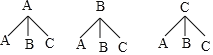
共有9种等可能性情况,两个人在一个班的有3种可能,
∴他们同班级的概率为![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
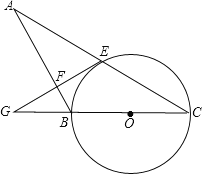
【题目】如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若GF=2![]() ,GB=4,求⊙O的半径.
,GB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=mx2+2mx+m﹣1(m≠0)与y轴交于点C,抛物线G的顶点为D,直线:y=mx+m﹣1(m≠0).

(1)当m=1时,画出直线和抛物线G,并直接写出直线被抛物线G截得的线段长.
(2)随着m取值的变化,判断点C,D是否都在直线上并说明理由.
(3)若直线被抛物线G截得的线段长不小于2,结合函数的图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
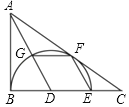
【题目】如图,在△ABC中,E为BC边上一点,以BE为直径的AR半圆D与AC相切于点F,且EF∥AD,AD交半圆D于点G.
(1)求证:AB是半圆D的切线;
(2)若EF=2,AD=5,求切线长AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com