
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
【答案】(1)A、B两种型号汽车的进货单价为:10万元、8万元;(2)A、B两种型号的汽车售价各为14万元、12万元时,每周销售这两种汽车的总利润最大,最大利润是32万元..
【解析】
(1)由题意根据购进两种型号的汽车数量相同列出分式方程即可求解;
(2)由题意根据销售利润等于每台汽车的利润乘以销售量列出二次函数关系即可求解.
解:(1)设B型汽车的进货单价为x万元,根据题意得![]() =
=![]() ,解得x=8,
,解得x=8,
经检验x=8是原分式方程的根.
答:A、B两种型号汽车的进货单价为:10万元、8万元.
(2)设两种汽车的总利润为w万元,根据题意得
w=(x+2﹣10)[﹣(x+2)+18]+(x﹣8)(﹣x+14)
=﹣2x2+48x﹣256
=﹣2(x﹣12)2+32
∵﹣2<0,当x=12时,w有最大值为32.
答:A、B两种型号的汽车售价各为14万元、12万元时,每周销售这两种汽车的总利润最大,最大利润是32万元.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
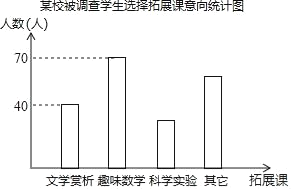
【题目】为丰富学生的课余生活,某校记划开展三种拓展课活动,分别是“文学赏析”,“趣味数学”,“科学实验”等项目,要求每位学生自主选择其中一项拓展课参加.随机抽取该校各年段部分学生,对选择拓展课的意向进行调査,将调查的结果制作成以下统计图和不完整的统计表.
某校被调查学生选择拓展课意向统计表
选择意向 | 所占百分比 |
文学赏析 |
|
趣味数学 | 35% |
科学实验 |
|
其它 | 30% |
(1)该校有2000名学生,请你估计大约有多少名学生参加科学实验拓展课,并补全统计表.
(2)该校参加科学实验拓展课的学生随机分成A,B,C三个人数相同的班级.小慧和小明都参加科学实验拓展课,求他们同班级的概率(画树状图或列表法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
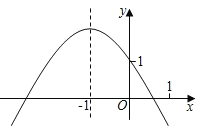
A.①②B.①③④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的三条角平分线交于一点,这个点称为三角形的内心(即三角形内切圆的圆心) . 现在规定,如果四边形的四条角平分线交于一点,我们把这个点称为“四边形的内心”.
问题提出
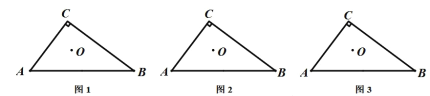
(1)如图1,在△ABC中,∠C=90°,点O为△ABC的内心,若直线DE分别交边AC、BC于点D、E,且点O仍然为四边形ABED的内心,这样的直线DE可以画多少条?请在图1中画出一条符合条件的直线DE,并简要说明画法.
问题探究
(2)如图2,在△ABC中,∠C=90°, AC=3, BC=4,若满足(1)中条件的一条直线DE // AB,求此时线段DE的长;
问题解决
(3)如图3,在△ABC中,∠C=90°, AC=3,BC=4,问满足(1)中条件的线段DE是否存在最小值?如果存在,请求出这个值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
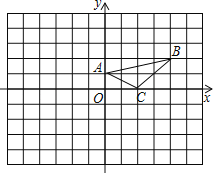
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
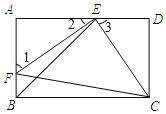
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)第1个等式:a1=![]() ; 第2个等式:a2=
; 第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ; 第4个等式:a4=
; 第4个等式:a4=![]() ;
;
…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.

(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本![]() (万元)与两个月游客总人数
(万元)与两个月游客总人数![]() (万人)之间满足函数关系式:
(万人)之间满足函数关系式:![]() ;两个月游客总人数
;两个月游客总人数![]() (万人)满足:
(万人)满足:![]() ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润![]() 门票收入
门票收入![]() 景区运营成本)
景区运营成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,点A,C分别在x轴、y轴的正半轴上,点B在第一象限内,四边形OABC是矩形,反比例函数y=![]() (x>0)与AB相交于点D,与BC相交于点E,若BE=4CE,四边形ODBE的面积是8,则k=_____.
(x>0)与AB相交于点D,与BC相交于点E,若BE=4CE,四边形ODBE的面积是8,则k=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com