
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
【答案】(1)A种机器人每个的进价是2万元,B种机器人每个的进价是4万元;(2)有如下两种方案:方案(1)购买A种机器人的个数是8个,则购买B种机器人的个数是20个;方案(2)购买A种机器人的个数是9个,则购买B种机器人的个数是22个.
【解析】分析:(1)、首先设A种机器人每个的进价是x万元,B种机器人每个的进价是y万元,根据题意列出二元一次方程组,从而得出答案;(2)、设购买A种机器人的个数是m个,则购买B种机器人的个数是(2m+4)个,根据题意列出不等式组,从而求出不等式组的解,根据解为整数得出方案.
详解:解:(1)、设A种机器人每个的进价是x万元,B种机器人每个的进价是y万元,依题意有:![]() , 解得:
, 解得:![]() .
.
故A种机器人每个的进价是2万元,B种机器人每个的进价是4万元;
(2)、设购买A种机器人的个数是m个,则购买B种机器人的个数是(2m+4)个,依题意有
![]() , 解得:8≤m≤9, ∵m是整数, ∴m=8或9,
, 解得:8≤m≤9, ∵m是整数, ∴m=8或9,
故有如下两种方案:
方案(1):m=8,2m+4=20,即购买A种机器人的个数是8个,则购买B种机器人的个数是20个;
方案(2):m=9,2m+4=22,即购买A种机器人的个数是9个,则购买B种机器人的个数是22个.


科目:初中数学 来源: 题型:
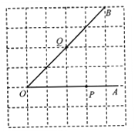
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中表示下面各点:
A(0,3) B(1,-3) C(3,-5) D(-3,-5) E(3,5).连接CE,CD.
(1)A点到原点的距离是___个单位长度;B点到直线CD的距离是____个单位长度;
(2)将点C向x轴的负方向平移6个单位,它与点_______重合;
(3)直线CE与y轴的位置关系是_______;直线CE与x轴的位置关系是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
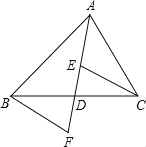
【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,a,b之间的距离为4,点P到直线a的距离为4,点Q到直线b的距离为2,PQ=2![]() .在直线a上有一动点A,直线b上有一动点B,满足AB⊥b,且PA+AB+BQ最小,此时PA+BQ=________.
.在直线a上有一动点A,直线b上有一动点B,满足AB⊥b,且PA+AB+BQ最小,此时PA+BQ=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°, AM⊥BC,垂足为M.
(1)如图1,若AB=4![]() ,BC=7,求AC的长;
,BC=7,求AC的长;
(2)如图2, 点D是线段AM上一点,MD=MC,点E是△ABC外一点,CE=CA,连接ED并延长交BC于点F,且∠BDF=∠CEF,
求证①AC=BD;
②BF=CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )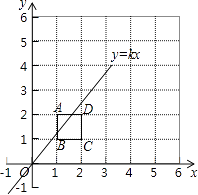
A.3
B.2
C.1
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com