
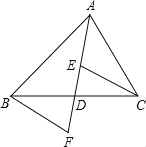
【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
【答案】①③
【解析】
根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,
∵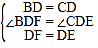 ,
,
∴△BDF≌△CDE(SAS),
∴∠F=∠DEC,
∴BF∥CE,故③正确;
∵△BDF≌△CDE,
∴CE=BF,故④错误,
正确的结论为:①③,
故答案为:①③.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+3的图象与反比例y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.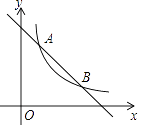
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与y轴交于点A,与x轴交于点B,过AB中点D的直线CD交x轴于点C,且经过第一象限的点E(6,4).
(1)求A,B两点的坐标及直线CD的函数表达式;
(2)连接BE,求△DBE的面积;
(3)连接DO,在坐标平面内找一点F,使得以点C,O,F为顶点的三角形与△COD全等,请直接写出点F的坐标.
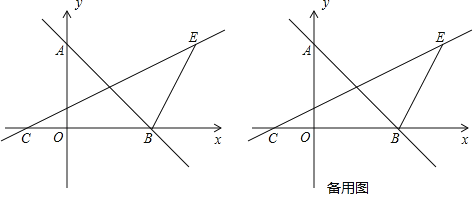
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF. 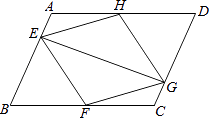
(1)求证:△AEH≌△CGF;
(2)求证:四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( ) ①m是无理数;
②m是方程m2﹣12=0的解;
③m满足不等式组 ![]() ;
;
④m是12的算术平方根.
A.①②
B.①③
C.③
D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com