
【题目】如图,一次函数y=﹣x+4的图象与y轴交于点A,与x轴交于点B,过AB中点D的直线CD交x轴于点C,且经过第一象限的点E(6,4).
(1)求A,B两点的坐标及直线CD的函数表达式;
(2)连接BE,求△DBE的面积;
(3)连接DO,在坐标平面内找一点F,使得以点C,O,F为顶点的三角形与△COD全等,请直接写出点F的坐标.
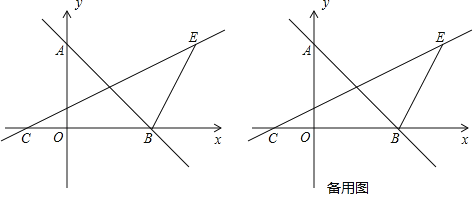
【答案】(1)A(0,4),B(4,0),y=![]() x+1;(2)6;(3)当点F在第一象限时,点F的坐标为(2,2);当点F在第二象限时,点F的坐标为(﹣4,2);当点F在第三象限时,点F的坐标为(﹣4,﹣2);当点F在第四象限时,点F的坐标为(2,﹣2).
x+1;(2)6;(3)当点F在第一象限时,点F的坐标为(2,2);当点F在第二象限时,点F的坐标为(﹣4,2);当点F在第三象限时,点F的坐标为(﹣4,﹣2);当点F在第四象限时,点F的坐标为(2,﹣2).
【解析】
(1)依据一次函数y=-x+4,求得A(0,4),B(4,0),依据D是AB的中点,可得D(2,2),运用待定系数法即可得到直线CD的函数表达式;
(2)先求得C(-2,0),BC=2=4=6,再根据△DBE的面积=△BCE的面积-△BCD的面积,进行计算即可;
(3)在四个象限内分别找到点F,使得以点C,O,F为顶点的三角形与△COD全等.
(1)一次函数y=﹣x+4,令x=0,则y=4;令y=0,则x=4,
∴A(0,4),B(4,0),
∵D是AB的中点,
∴D(2,2),
设直线CD的函数表达式为y=kx+b,则![]() ,解得
,解得 ,
,
∴直线CD的函数表达式为y=![]() x+1;
x+1;
(3)y=![]() x+1,令y=0,则x=﹣2,
x+1,令y=0,则x=﹣2,
∴C(﹣2,0),
∴BC=2=4=6,
∴△DBE的面积=△BCE的面积﹣△BCD的面积=![]() ×6×(4﹣2)=6;
×6×(4﹣2)=6;
(3)如图所示,

当点F在第一象限时,点F与点D重合,即点F的坐标为(2,2);
当点F在第二象限时,点F的坐标为(﹣4,2);
当点F在第三象限时,点F的坐标为(﹣4,﹣2);
当点F在第四象限时,点F的坐标为(2,﹣2).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
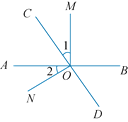
【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 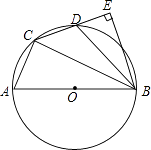
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度. 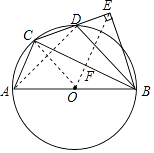
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费标准如下:行驶路程不超过3千米时,收费8元;行驶路程超过3千米的部分,按每千米1.60元计费.
(1)求出租车收费y(元)与行驶路程x(千米)之间的函数关系式;
(2)若某人一次乘出租车时,付出了车费14.40元,求他这次乘坐了多少千米的路?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
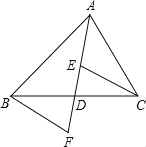
【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
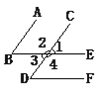
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com