
【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

【答案】(1)(1)同旁内角互补,两直线平行;平行于同一直线的两条直线互相平行;两直线平行,同旁内角互补;(2)∠BDF=∠B+∠F,理由见解析;(3)∠BDF=∠F-∠B.
【解析】试题分析:(1)根据平行线的性质和判定填空即可;
(2)过点D作AB的平行线DC,根据两直线平行,内错角相等证明即可;
(3)与(2)的证明方法类似,可以求出![]() 与
与![]() 的数量关系.
的数量关系.
试题解析:因为![]()
所以AB∥EF(同旁内角互补,两直线平行),
因为AB∥CD(已知),
所以CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也平行),
所以![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
所以![]()
(2)过点D作AB的平行线DC,

因为AB∥EF,
所以∠B=∠BDC,
因为AB∥EF,
所以CD∥EF,
所以∠F=∠FDC,
所以∠BDF=∠B+∠F
(3)过点D作AB的平行线DC,
根据平行线的性质可以证明图③∠BDF+∠B=∠F;图④∠BDF+∠B=∠F.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
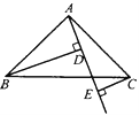
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
(1)AD与CE的大小关系如何?请说明理由;
(2)若BD=5,CE=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图1和图2的统计图.请回答下列问题:
(1)该班共有多少名学生?
(2)求图1中“乒乓球”部分的人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)求出扇形统计图中表示“足球”的扇形的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
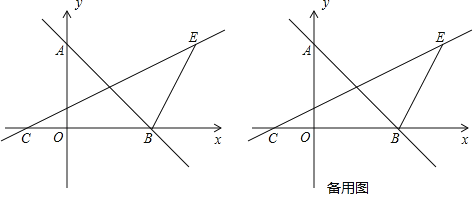
【题目】如图,一次函数y=﹣x+4的图象与y轴交于点A,与x轴交于点B,过AB中点D的直线CD交x轴于点C,且经过第一象限的点E(6,4).
(1)求A,B两点的坐标及直线CD的函数表达式;
(2)连接BE,求△DBE的面积;
(3)连接DO,在坐标平面内找一点F,使得以点C,O,F为顶点的三角形与△COD全等,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
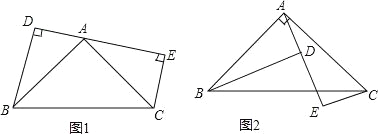
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
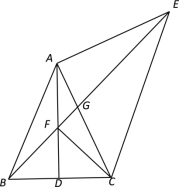
【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠. 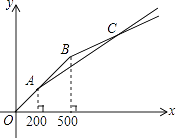
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com