
【题目】为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图1和图2的统计图.请回答下列问题:
(1)该班共有多少名学生?
(2)求图1中“乒乓球”部分的人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)求出扇形统计图中表示“足球”的扇形的圆心角度数.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
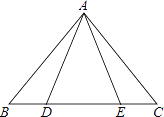
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H. 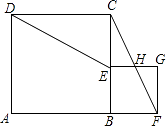
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 ,中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面内有4个点A(0,2),B(-2,0),C(1,-1),D(3,1).
(1)建立坐标系,描出这4个点;
(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.
(3)线段AB,CD有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= ![]() AB.
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,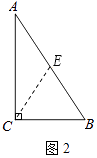
CE与AB相交于点E.
∵∠BCE=∠B,
∴ .
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵ ,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE= ![]() AB.
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD= ![]() AB.
AB.
请把证法1补充完整,并用不同的方法完成证法2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC. 
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com