
【题目】如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H. 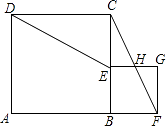
(1)若E是BC的中点,求证:DE=CF;
(2)若∠CDE=30°,求 ![]() 的值.
的值.
【答案】
(1)证明:∵E是BC的中点,
∴BE=CE,
在正方形ABCD和正方形BFGE中,BC=CD,BE=BF,
∴BF=CE,
在△BCF和△CDE中,  ,
,
∴△BCF≌△CDE(SAS),
∴DE=CF
(2)解:设CE=x,∵∠CDE=30°,
∴tan∠CDE= ![]() =
= ![]() ,
,
∴CD= ![]() x,
x,
∵正方形ABCD的边BC=CD,
∴BE=BC﹣CE= ![]() x﹣x,
x﹣x,
∵正方形BFGE的边长BF=BE,
∴tan∠BCF= ![]() =
= ![]() =
= ![]() ,
,
∵正方形BGFE对边BC∥GF,
∴∠BCF=∠GFH,
∵tan∠GFH= ![]() ,
,
∴ ![]() =
= ![]()
【解析】(1)根据线段中点的定义可得BE=CE,再根据正方形的四条边都相等可得BC=CD,BE=BF,然后求出BF=CE,再利用“边角边”证明△BCF和△CDE全等,根据全等三角形对应边相等可得DE=CF;(2)设CE=x,根据∠CDE的正切值表示出CD,然后求出BE,从而得到∠BCF的正切值,再根据两直线平行,内错角相等可得∠BCF=∠GFH,然后根据等角的正切值相等解答即可.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
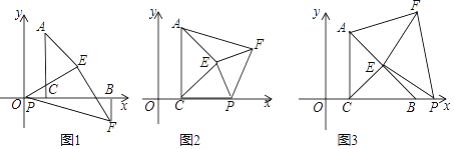
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图①,在△ABC 中,D、E 分别是 AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点 A 顺时针旋转一定角度,连接 BD,CE,得到图②,将 BD、CE 分别延长至 M、N,使 DM=![]() BD,EN=
BD,EN=![]() CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)在图②中,BD 与 CE 的数量关系是 ;
(2)在图③中,猜想 AM 与 AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ ![]() x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.
x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.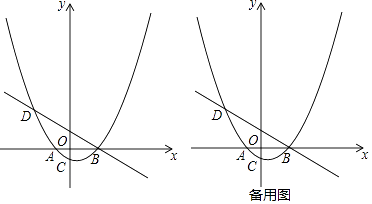
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图1和图2的统计图.请回答下列问题:
(1)该班共有多少名学生?
(2)求图1中“乒乓球”部分的人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)求出扇形统计图中表示“足球”的扇形的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D为BC边上一点.
(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4 ![]() ,BC=6,∠B=45°,则CD的取值范围是 .
,BC=6,∠B=45°,则CD的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com