
【题目】在平面直角坐标系中表示下面各点:
A(0,3) B(1,-3) C(3,-5) D(-3,-5) E(3,5).连接CE,CD.
(1)A点到原点的距离是___个单位长度;B点到直线CD的距离是____个单位长度;
(2)将点C向x轴的负方向平移6个单位,它与点_______重合;
(3)直线CE与y轴的位置关系是_______;直线CE与x轴的位置关系是_______.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
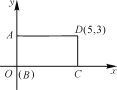
【题目】已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点A的坐标是______,点B的坐标是______,点C的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
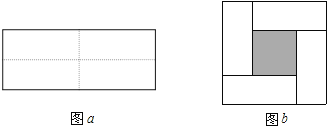
【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,
则(a-b)2= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河边有两个村庄A、B,要在河边建一自来水厂向A村与B村供水。
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P,Q两点停止运动.
(1)AC= cm,BC= cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,P与Q第一次相遇;
(4)当t为何值时,PQ=1cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.
四边形 | 对称性 | 边 | 角 | 对角线 |
平行 | . | 两组对边分别平行,两组对边分别相等. | 两组对角 | 对角线互相平分. |
等腰 | 轴对称图形,过平行的一组对边中点的直线是它的对称轴. | 一组对边平行,另一组对边相等. | . | . |
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.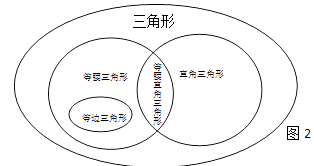
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com