
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
科目:初中数学 来源: 题型:
【题目】如图,小河边有两个村庄A、B,要在河边建一自来水厂向A村与B村供水。
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
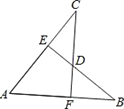
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路边安装路灯,灯柱BC高15m,与灯杆AB的夹角ABC为120°.路灯采用锥形灯罩,照射范围DE长为18.9m,从D、E两处测得路灯A的仰角分别为∠ADE=80.5°,∠AED=45°.求灯杆AB的长度.(参考数据:cos80.5°≈0.2,tan80.5°≈6.0)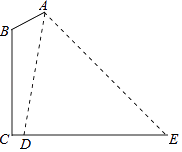
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.
四边形 | 对称性 | 边 | 角 | 对角线 |
平行 | . | 两组对边分别平行,两组对边分别相等. | 两组对角 | 对角线互相平分. |
等腰 | 轴对称图形,过平行的一组对边中点的直线是它的对称轴. | 一组对边平行,另一组对边相等. | . | . |
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.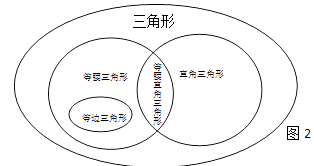
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com