
【题目】在△ABC中,∠B=45°, AM⊥BC,垂足为M.
(1)如图1,若AB=4![]() ,BC=7,求AC的长;
,BC=7,求AC的长;
(2)如图2, 点D是线段AM上一点,MD=MC,点E是△ABC外一点,CE=CA,连接ED并延长交BC于点F,且∠BDF=∠CEF,
求证①AC=BD;
②BF=CF.

【答案】(1)5;(2)见解析.
【解析】
(1)先由AM=BM=ABcos45°=4可得CM=3,再由勾股定理可得AC的长;
(2)①由AM⊥BC,得∠AMC=∠BMD=90°,再由三角形全等可证AC=BD;
②延长EF到点G,作BG∥EC,可得∠G=∠CEF,证得BG=CE,再证△BFG≌△CFE可得BF=CF.
(1)解:∵AM⊥BC,
∴∠AMB=90°.
∵∠B=45°,
∴∠BAM=90°-45°=45°.
∴BM=AM.
∵AB=![]() ,
,
∴BM=4.
∴CM=BC-BM=3.
∵∠AMC=90°,
∴AC=![]() .
.
(2)①∵AM⊥BC,
∴∠AMC=∠BMD=90°.
∵MC=MD,AM=BM,
∴△AMC≌△BMD.
∴AC=BD.
②延长EF,过B作BG∥EC交EF延长线于点G.
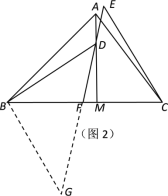
∵BG∥CE,
∴∠G=∠CEF.
∵∠BDF=∠CEF,
∴∠G=∠BDF.
∴BG=BD.
∵AC=CE,AC=BD,
∴BG=CE.
∵∠BFG=∠CFE,
∴△BGF≌△CEF.
∴BF=CF.


科目:初中数学 来源: 题型:
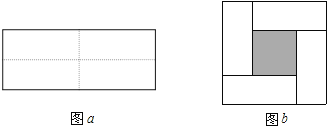
【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,
则(a-b)2= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF. 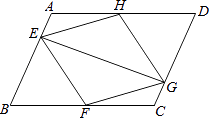
(1)求证:△AEH≌△CGF;
(2)求证:四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
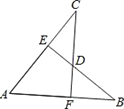
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.
四边形 | 对称性 | 边 | 角 | 对角线 |
平行 | . | 两组对边分别平行,两组对边分别相等. | 两组对角 | 对角线互相平分. |
等腰 | 轴对称图形,过平行的一组对边中点的直线是它的对称轴. | 一组对边平行,另一组对边相等. | . | . |
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.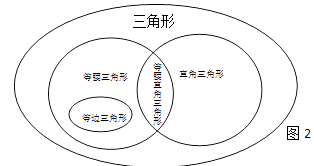
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com