
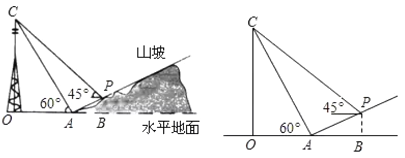
【题目】如图,某人在山坡坡脚![]() 处测得电视塔尖点
处测得电视塔尖点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得点
处再测得点![]() 的仰角为
的仰角为![]() ,已知
,已知![]() 米,山坡坡度
米,山坡坡度![]() ,且
,且![]() 在同一条直线上,其中测倾器高度忽略不计.
在同一条直线上,其中测倾器高度忽略不计.
(1)求电视塔![]() 的高度;(计算结果保留根号形式)
的高度;(计算结果保留根号形式)
(2)求此人所在位置点![]() 的铅直高度.(结果精确到0.1米,参考数据:
的铅直高度.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
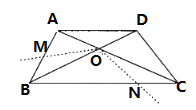
【题目】如图,四边形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC.
(1)求出sin∠DBC的值;
(2)若AD=2,把∠BOC绕点O顺时针旋转![]() (
(![]() ),交AB于点M,交BC于点N(如图),求证:四边形OMBN的面积为一个定值,并求出这个定值.
),交AB于点M,交BC于点N(如图),求证:四边形OMBN的面积为一个定值,并求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育学业考试成绩统计表如下:
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x1x2+y1y2=0,且A,B均不为原点,则称A和B互为正交点.比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互为正交点.
(1)点P和Q互为正交点,P的坐标为(﹣2,3),
①如果Q的坐标为(6,m),那么m的值为多少;
②如果Q的坐标为(x,y),求y与x之间的关系式;
(2)点M和N互为正交点,直接写出∠MON的度数;
(3)点C,D是以(0,2)为圆心,半径为2的圆上的正交点,以线段CD为边,构造正方形CDEF,圆心F在正方形CDEF的外部,求线段OE长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com