
【题目】在新中国成立70周年之际,某校开展了“校园文化艺术”活动,活动项目有:书法、绘画、声乐和器乐,要求全校学生人人参加,并且每人只能参加其中一项活动,政教处在该校学生中随机抽取了100名学生进行调查和统计,并绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题:
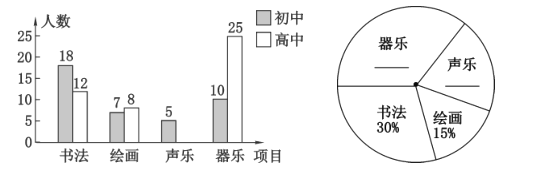
(1)请补全条形统计图和扇形统计图;
(2)该校初中学生中,参加“书法”项目的学生所占的百分比是多少?
(3)若该校共有1500人,请估计其中参加“器乐”项目的高中学生有多少人?
(4)经政教处对所有参加“绘画”项目的作品进行评比,共选出2名初中学生和2名高中学生的最佳作品,学校决定从这4名学生中随机抽取2人作为学生会“绘画社团”的团生,那么正好抽到一名初中学生和一名高中学生的概率是多少?
【答案】(1)详见解析;(2)45%;(3)约有375人;(4)![]()
【解析】
(1)先根据总人数100人求出参加声乐的高中学生人数,再分别算出参加器乐和声乐的人数占总人数的百分比,最后补全条形统计图和扇形统计图即可;
(2)先求出100名学生中初中学生的总人数,然后即可求得“书法”项目的学生所占的百分比;
(3)先求出参加“器乐”项目的高中学生占总人数的百分比,进而可求得全校参加“器乐”项目的高中学生人数;
(4)列表得出所有等可能的情况数,找出所选4名同学中正好抽到一名初中学生和一名高中学生的情况,即可求出所求概率.
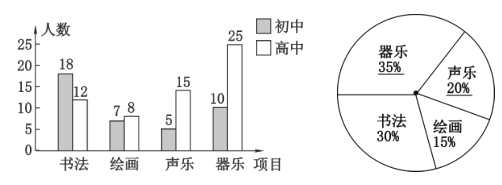
解:(1)100﹣18﹣12﹣7﹣8﹣5﹣10﹣25=15(人),
(10+25)÷100=35%,
(5+15)÷100=20%,
补全条形统计图和扇形统计图如下:
(2)![]() ,
,
答:该校初中学生中,参加“书法”项目的学生占45%.
(3)![]() (人)
(人)
答:该校参加“器乐”项目的高中学生约有375人.
(4)记两名高中学生为![]() ,两名初中学生为
,两名初中学生为![]() ,列表如下:
,列表如下:
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
由上表可知,共有12种等可能结果,其中能抽到一名初中学生和一名高中学生的结果有8种,
∴![]() (抽一名初中学生和一名高中学生)
(抽一名初中学生和一名高中学生)![]() ,
,
答:正好抽到一名初中学生和一名高中学生的概率是![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△CDE都是等腰三角形,∠BAC=∠EDC=120°.
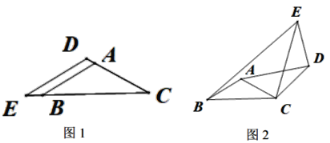
(1)如图1,A、D、C在同一直线上时,![]() =_______,
=_______,![]() =_______;
=_______;
(2)在图1的基础上,固定△ABC,将△CDE绕C旋转一定的角度α(0°<α<360°),如图2,连接AD、BE.
① ![]() 的值有没有改变?请说明理由.
的值有没有改变?请说明理由.
②拓展研究:若AB=1,DE=![]() ,当 B、D、E在同一直线上时,请计算线段AD的长;
,当 B、D、E在同一直线上时,请计算线段AD的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,点D是AB上一点,以BD为直径的⊙0与AC边相切于点E,交BC于点F,FG⊥AC于点G.
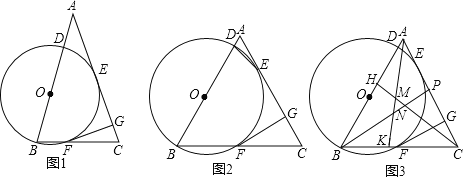
(1)如图l,求证:GE=GF;
(2)如图2,连接DE,∠GFC=2∠AED,求证:△ABC为等边三角形;
(3)如图3,在(2)的条件下,点H、K、P分别在AB、BC、AC上,AK、BP分别交CH于点M、N,AH=BK,∠PNC﹣![]() ∠BAK=60°,CN=6,CM=4
∠BAK=60°,CN=6,CM=4![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
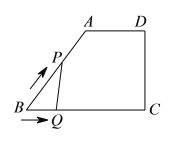
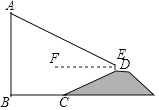
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 以
以![]() 的速度沿折线
的速度沿折线![]() 运动到点
运动到点![]() ,点
,点![]() 以
以![]() 的速度沿
的速度沿![]() 运动到点
运动到点![]() ,设
,设![]() ,
,![]() 同时出发
同时出发![]() 时,
时,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致是( )
的函数图象大致是( )
A. 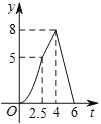 B.
B. 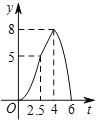
C. 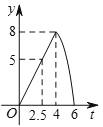 D.
D. 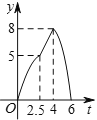
查看答案和解析>>
科目:初中数学 来源: 题型:
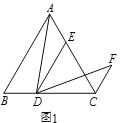
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
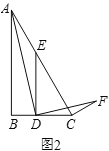
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
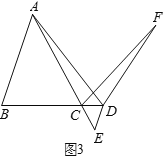
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,![]() .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角
.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角![]() 为
为![]() (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)
(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)![]() ,那么建筑物AB的高度约为( )
,那么建筑物AB的高度约为( )
(参考数据![]() ,
,![]() ,
,![]() )
)
A.65.8米B.71.8米C.73.8米D.119.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数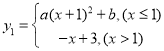 (
(![]() 为常数且
为常数且![]() ),已知当
),已知当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,请对该函数及其图像进行如下探究:
,请对该函数及其图像进行如下探究:

(1)求函数![]() 的解析式;
的解析式;
(2)如图,请在平面直角坐标系中,画出该函数的图像;
(3)结合所画函数图像,请写出该函数的一条性质;
(4)解决问题:若函数![]() 与
与![]() 至少有两个公共点,请直接写出
至少有两个公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
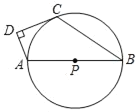
【题目】如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,2∠B+∠DAB=180°.
(1)证明:直线CD为⊙P的切线;
(2)若DC=2![]() ,AD=4,求⊙P的半径.
,AD=4,求⊙P的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com