
(本题满分8分)动手实验:利用矩形纸片(图1)剪出一个正六边形纸片;利用这个正六边形纸片做一个如图(2)无盖的正六棱柱(棱柱底面为正六边形);
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
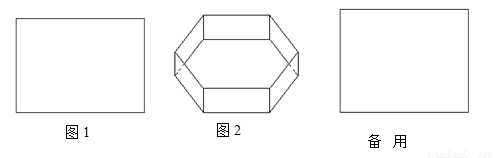
(2)在(1)的前提下,当矩形的长为2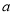 时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率=
时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率= 无盖正六棱柱的表面积/矩形纸片的面积)
无盖正六棱柱的表面积/矩形纸片的面积)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年山东省枣庄市中考第三次适应性训练数学试卷(解析版) 题型:填空题
已知一组数据1,a,3,6,7,它的平均数是4,这组数据的中位数是____.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次调研考试数学试卷(解析版) 题型:解答题
(本题满分12分)点P为抛物线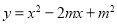 (m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图像与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图像与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
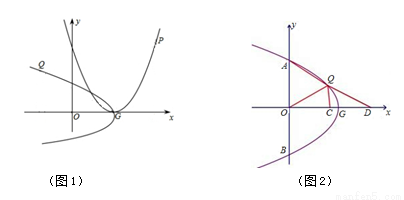
(1)如图(1)当m=2,点P横坐标为4时,求Q点的坐标;
(2)设点Q(a,b),用含m、b的代数式表示a;
(3)如图(2),点Q在第一象限内,点D在x轴的正半轴上,点C为OD的中点,QO平分∠AQC,AQ=2QC,当QD=m时,求m的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次调研考试数学试卷(解析版) 题型:选择题
从北京教育考试院获悉,2015年北京中考预计报名人数达8.9万人 ,8.9万这个数据用科学记数法表示为( )
A.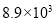 B.
B.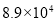 C.
C. D.
D.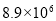
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级中考一模数学试卷(解析版) 题型:解答题
(本题8分)某校八年级所有学生参加2013年初中生物竞赛,我们从中随机抽取了部分学生的考试成绩,将他们的成绩进行统计后分为A、B、C、D四等,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
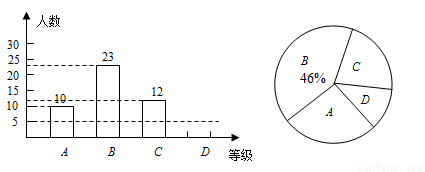
(说明:A级:25分~30分;B级:20分~24分;C级:15分~19分;D级:15分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所占的百分比是 _______ ;
(3)扇形统计图中A级所在的扇形的圆心角度数是 _______ ;
(4)若该校九年级有850名学生,请你估计全年级A级和B级的学生人数共约为 ______ 人.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级中考一模数学试卷(解析版) 题型:填空题
某小组8位学生一次数学测试的分数为121,123,123,124,126,127,128,128,那么这个小组测试分数的标准差是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市天一实验学校九年级中考一模数学试卷(解析版) 题型:解答题
(本题满分10分)对于半径为r的⊙P及一个正方形给出如下定义:若⊙P上存在到此正方形四条边距离都相等的点,则称⊙P是该正方形的“等距圆”.如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
(1)当r=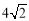 时,
时,
①在P1(0,-3),P2(4,6),P3(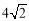 ,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
②若点P在直线 上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
(2)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(6,2),顶点E、H在y轴上,且点H在点E的上方.
①若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P 在y轴上截得的弦长;
②将正方形ABCD绕着点D旋转一周,在旋转的过程中,线段HF上没有一个点能成为它的“等距圆”的圆心,则r的取值范围是_______________ .
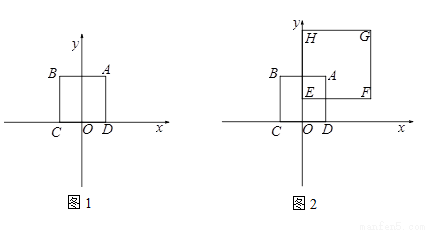
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com