
(本题满分10分)对于半径为r的⊙P及一个正方形给出如下定义:若⊙P上存在到此正方形四条边距离都相等的点,则称⊙P是该正方形的“等距圆”.如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
(1)当r=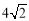 时,
时,
①在P1(0,-3),P2(4,6),P3(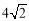 ,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
,2)中可以成为正方形ABCD的“等距圆”的圆心的是_______________;
②若点P在直线 上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
(2)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(6,2),顶点E、H在y轴上,且点H在点E的上方.
①若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P 在y轴上截得的弦长;
②将正方形ABCD绕着点D旋转一周,在旋转的过程中,线段HF上没有一个点能成为它的“等距圆”的圆心,则r的取值范围是_______________ .
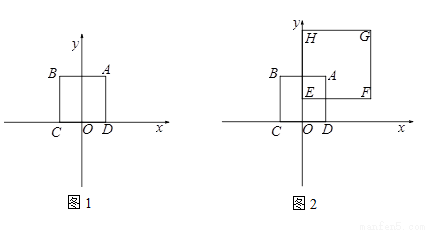
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区九年级第一次模拟数学试卷(解析版) 题型:填空题
某校安排三辆车,组织九年级学生去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级中考一模数学试卷(解析版) 题型:解答题
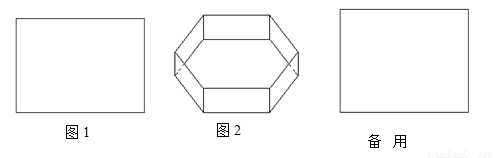
(本题满分8分)动手实验:利用矩形纸片(图1)剪出一个正六边形纸片;利用这个正六边形纸片做一个如图(2)无盖的正六棱柱(棱柱底面为正六边形);
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的前提下,当矩形的长为2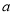 时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率=
时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率?(矩形纸片的利用率= 无盖正六棱柱的表面积/矩形纸片的面积)
无盖正六棱柱的表面积/矩形纸片的面积)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级中考一模数学试卷(解析版) 题型:选择题
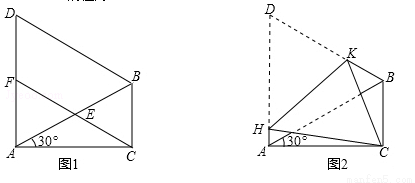
如图1,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,E是AB的中点,连结CE并延长交AD于F,如图2,现将四边形ACBD折叠,使D与C重合,HK为折痕,则sin∠ACH的值为( )
A.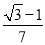 B.
B.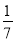 C.
C.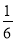 D.
D.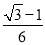
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市天一实验学校九年级中考一模数学试卷(解析版) 题型:解答题
(本题满分7分)如图,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,连接DE.
证明:DF=DC.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市天一实验学校九年级中考一模数学试卷(解析版) 题型:填空题
若关于x的一元二次方程kx2+2(k+1)x+k-1=0有两个实数根,则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)已知:如图,矩形ABCD中,CD=2,AD=3,以C点为圆心,作一个动圆,与线段AD交于点P(P和A、D不重合),过P作⊙C的切线交线段AB于F点.
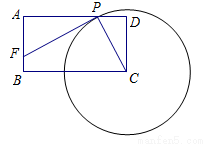
(1)求证:△CDP∽△PAF;
(2)设DP=x,AF=y,求y关于x的函数关系式,及自变量x的取值范围;
(3)是否存在这样的点P,使△APF沿PF翻折后,点A落在BC上,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com