
 如图,已知⊙O过边长为4的正方形ABCD顶点A、B.
如图,已知⊙O过边长为4的正方形ABCD顶点A、B.分析 (1)①如图1中,作线段AB的垂直平分线EF,交CD于F,连接AF,作线段AF的垂直平分线MN交EF于点O,以点O为圆心,OA的长为半径作⊙O,⊙O即为所求.②如图2中,设⊙O与AD、DC分别交于点E、F,FO的延长线交AB于M,设OA=x,则AM=2,FO=x,OM=4-x,在Rt△AMO中,根据OA2=OM2+AM2,列出方程求解即可.
(2)①如图3中,当△DEN∽△MFA时,设AG=GE=OM=a,AE=FN=2a,由NM=4,得3a+r=4 ①在Rt△AOM中,由OA2=OM2+AM2,得22+a2=r2 ②,解方程组即可解决问题.②如图4中,当⊙O与CD相切时,连接BN.只要证明△DEN∽△MAN,即可解决问题.
解答 解:(1)①如图1中,作线段AB的垂直平分线EF,交CD于F,连接AF,作线段AF的垂直平分线MN交EF于点O,以点O为圆心,OA的长为半径作⊙O,⊙O即为所求.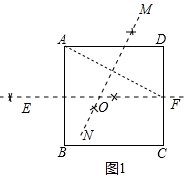
②如图2中,设⊙O与AD、DC分别交于点E、F,FO的延长线交AB于M,设OA=x,则AM=2,FO=x,OM=4-x,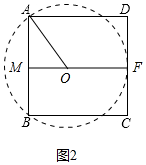
在Rt△AMO中,∠AMD=90°,OA2=OM2+AM2,
∴x2=22+(4-x)2,解得x=2.5,
∴⊙O的半径为2.5.
(2)①如图3中,当△DEN∽△MFA时,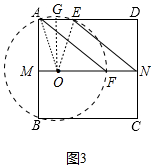
∵AM=DN,
∴△DEN≌△MFA,
∴FM=DE,AE=FN,设⊙O的半径为r,OM=a,
∵OA=OE,OG⊥AE,
∴AG=GE,
∵四边形AMOG是矩形,
∴AG=GE=OM=a,AE=FN=2a,
∵NM=4,
∴3a+r=4 ①
在Rt△AOM中,∵OA2=OM2+AM2,
∴22+a2=r2 ②,
由①②可得r=$\frac{3\sqrt{3}-1}{2}$.
②如图4中,当⊙O与CD相切时,连接BN.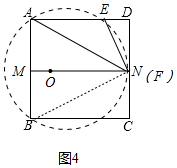
∵∠DEN+∠AEN=180°,∠ABN+∠AEN=180°,
∴∠DEN=∠ABN,
∵OM⊥AB,
∴$\widehat{AN}$=$\widehat{BN}$,
∴∠BAN=∠ABN=∠DEN,∵∠EDN=∠AMN,
∴△DEN∽△MAN,
由(1)可知此时⊙O的半径为2.5.
点评 本题考查圆综合题、正方形的性质、相似三角形的判定和性质、勾股定理的等知识,解题的关键是灵活运用所学知识,学会利用参数,构建方程以及方程组解决问题,属于中考压轴题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲数的3倍与乙数的$\frac{1}{2}$的和 | B. | a与1的差的$\frac{1}{4}$ | ||
| C. | 一个数的2倍比3小1 | D. | a与b的和的$\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15吨 | B. | 12$\frac{1}{5}$吨 | C. | 15$\frac{1}{5}$吨 | D. | 3$\frac{1}{5}$吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两城市相距80km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两城市相距80km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A是第一象限内的点,坐标为(4,y),OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$,求点A的坐标及α的余弦值.
如图,点A是第一象限内的点,坐标为(4,y),OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$,求点A的坐标及α的余弦值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
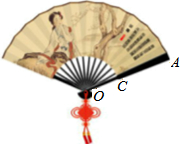 中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).
中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
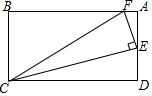 已知,如图,在矩形ABC中.E是AD的中点,EF⊥EC交AB于点F,连FC(AB>AE),求证:$\frac{DE}{AB}$=$\frac{AF}{DE}$.
已知,如图,在矩形ABC中.E是AD的中点,EF⊥EC交AB于点F,连FC(AB>AE),求证:$\frac{DE}{AB}$=$\frac{AF}{DE}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com