
 如图,A、B两城市相距80km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,A、B两城市相距80km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) 分析 过点P作PM⊥AB,M是垂足.AM与BM就都可以根据三角函数用PPM表示出来.根据AB的长,得到一个关于PM的方程,解出PM的长.从而判断出这条高速公路会不会穿越保护区.
解答 解:作PM⊥AB,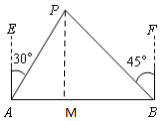
由题意得:AE∥PM∥BF,
∴∠APM=30°,∠BPM=45°,
∴PM=$\frac{AM}{tan∠APM}$=$\sqrt{3}$AM,BM=PM,
设BM=PM=x,则AM=$\frac{\sqrt{3}}{3}$x,
∴$\frac{{\sqrt{3}}}{3}x+x=80$
∴x=120-40$\sqrt{3}$≈50.72>50,
∴这条高速公路不会穿越保护区.
点评 本题主要考查解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x.
如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,点C为点B关于点A的对称点,设点C所表示的数为x.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
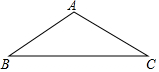 如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )
如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )| A. | 10sinα米 | B. | 10cosα米 | C. | 20sinα米 | D. | 20cosα米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O过边长为4的正方形ABCD顶点A、B.
如图,已知⊙O过边长为4的正方形ABCD顶点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com