ŌĶĮĻĀĆę²ÄĮĻ£¬²¢½ā“šĻĀĮŠø÷Ģā£ŗ
ŌŚŠĪČēa
b=NµÄŹ½×ÓÖŠ£¬ĪŅĆĒŅŃ¾ŃŠ¾æ¹żĮ½ÖÖĒéæö£ŗ
¢ŁŅŃÖŖaŗĶb£¬ĒóN£¬ÕāŹĒ³Ė·½ŌĖĖć£»
¢ŚŅŃÖŖbŗĶN£¬Ēóa£¬ÕāŹĒæŖ·½ŌĖĖć£»
ĻÖŌŚĪŅĆĒŃŠ¾æµŚČżÖÖĒéæö£ŗŅŃÖŖaŗĶN£¬Ēób£¬ĪŅĆĒ°ŃÕāÖÖŌĖĖć½Š×ö¶ŌŹżŌĖĖć£®
¶ØŅå£ŗČē¹ūa
b=N£Øa£¾0£¬a”Ł1£¬N£¾0£©£¬Ōņb½Š×öŅŌaĪŖµ×NµÄ¶ŌŹż£¬¼Ē×Åb=log
aN£®
ĄżČē£ŗŅņĪŖ2
3=8£¬ĖłŅŌlog
28=3£»ŅņĪŖ
2-3=£¬ĖłŅŌ
log2=-3£®
£Ø1£©øł¾Ż¶ØŅå¼ĘĖć£ŗ
¢Łlog
381=
£»¢Ślog
33=
£»¢Ūlog
31=
£»
¢ÜČē¹ūlog
x16=4£¬ÄĒĆ“x=
£®
£Ø2£©Éča
x=M£¬a
y=N£¬Ōņlog
aM=x£¬log
aN=y£Øa£¾0£¬a”Ł1£¬M”¢N¾łĪŖÕżŹż£©£¬
ӧa
x•a
y=a
x+y£¬”ąa
x+y=M•N”ąlog
aMN=x+y£¬
¼“log
aMN=log
aM+log
aN
ÕāŹĒ¶ŌŹżŌĖĖćµÄÖŲŅŖŠŌÖŹÖ®Ņ»£¬½ųŅ»²½£¬ĪŅĆĒ»¹æÉŅŌµĆ³ö£ŗ
log
aM
1M
2M
3”M
n=
£ØĘäÖŠM
1ӢM
2ӢM
3”¢””¢M
n¾łĪŖÕżŹż£¬a£¾0£¬a”Ł1£©
log
a=
£Øa£¾0£¬a”Ł1£¬M”¢N¾łĪŖÕżŹż£©£®

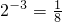 £¬ĖłŅŌ
£¬ĖłŅŌ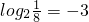 £®
£®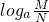 £¬²¢ĖµĆ÷ĄķÓÉ£®
£¬²¢ĖµĆ÷ĄķÓÉ£®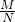 £¬
£¬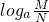 =x-y=logaM-logaN£®
=x-y=logaM-logaN£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
 £»
£» £»
£» .
. µÄ½į¹ū £»
µÄ½į¹ū £» = £¬“ĖŹ±³Ę
= £¬“ĖŹ±³Ę Óė
Óė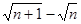 »„ĪŖÓŠĄķ»ÆŅņŹ½£»
»„ĪŖÓŠĄķ»ÆŅņŹ½£»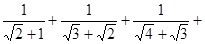 ”+
”+  ”£
ӣ