
����Ŀ���������ڼ䣬ij��λ��֯����λ����ְ��ǰȥ��������480ǧ����������ɽ�Ǹ����Σ����������϶࣬�����üס���������;������ͬһ·�߸ϸ����㣮ͼ�е����ߡ��߶ηֱ��ʾ�ס����������ߵ�·��y����ǧ�ף���y����ǧ�ף���ʱ��x��Сʱ��֮��ĺ�����ϵ��Ӧ��ͼ�������ͼ�����ṩ����Ϣ������������⣺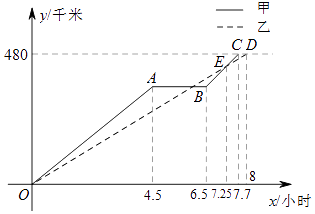
��1�����������������ϣ��׳���;��ͣ����Сʱ��
��2���׳��ų����Ϻ��������ٸ������㣮���ʼ׳����ų�����ʱ����������·���Ƕ���ǧ�ף�
��3��Ϊ�˱�֤��ʱ���磬�ס��ҳ��ڵ�һ������ʱԼ���˺�����֮���·�̲�����35ǧ�ף���ͨ������˵������ͼ������ʾ���߷��Ƿ����Լ����
���𰸡�
��1��2
��2��
�⣺������ֱ��OD�Ľ���ʽΪy=60x����ֱ��BC�Ľ���ʽΪy=kx+b��
��E��7.25��435����C��7.7��480����
���� ![]() �����
����� ![]() ��
��
��y=100x��290��
x=6.5ʱ��y=360��
��׳����ų�����ʱ����������·����360ǧ��
��3��
�⣺����Լ����
��ͼ���֪������������ͥ��һ����������B��C�����Զ��
�ڵ�B����y����y��=60��6.5��360=30ǧ�ף�35ǧ�ף�
�ڵ�C����y����y��=100��7.7��290����60��7.7��=18ǧ�ף�35ǧ�ף�
�ఴͼ������ʾ���߷�����Լ����
���������⣺��1���۲�ͼ���֪���׳���;��ͣ����6.6��4.5=2Сʱ��
���Դ���2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+b�뷴��������y= ![]() ��ͼ�ν���A��a��4����B��4��1�����㣮
��ͼ�ν���A��a��4����B��4��1�����㣮 
��1����b��k��ֵ��
��2���ڵ�һ�����ڣ���һ�κ���y=��x+b��ֵ���ڷ���������y= ![]() ��ֵʱ��ֱ��д���Ա���x��ȡֵ��Χ��
��ֵʱ��ֱ��д���Ա���x��ȡֵ��Χ��
��3����ֱ��y=��x+b����ƽ��m����λ����ֱ����˫����ֻ��һ������ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ֱ��y= ![]() x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ���ϵ�һ�㣬���ı���MAOC�͡�BOC������ֱ�ΪS�ı���MAOC��S��BOC �� ��S=S�ı���MAOC��S��BOC �� ��S���ʱ��M�����꼰S�����ֵ��
��3����ͼ�ڣ���������F1��y�ᷭ�۲������ơ��õ�������F2 �� ��A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA�䡢B�䡢M�䣬����M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A�䡢D��PΪ��������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ADΪֱ���İ�ԲO����Rt��ABC��б��AB�������˵㣬��ֱ�DZ�AC�ڵ�E��B��E�ǰ�Բ�������ȷֵ㣬��BE�ij�Ϊ ![]() ����ͼ����Ӱ���ֵ����Ϊ ��
����ͼ����Ӱ���ֵ����Ϊ �� 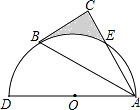
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͼ�����ش�������
(1)��һ����ǡ�ABC(���߾������)��
(2)����BC���ϵ�����AE��AD��
(3)д��������ADΪ�ߵ������Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCΪ�ȱ������Σ���DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ��������ADEF��ʹ��DAF=60�㣬����CF��
������֪��
��1����ͼ1������D�ڱ�BC��ʱ������֤����ADB=��AFC������ֱ���жϽ��ۡ�AFC=��ACB+��DAC�Ƿ������
��2����ͼ2������D�ڱ�BC���ӳ�����ʱ�������������䣬���ۡ�AFC=��ACB+��DAC�Ƿ��������д����AFC����ACB����DAC֮����ڵ�������ϵ����д��֤�����̣�
��3����ͼ3������D�ڱ�CB���ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC����࣬�����������䣬�벹ȫͼ�Σ���ֱ��д����AFC����ACB����DAC֮����ڵĵ�����ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����֯���Ż����ί������15ԪǮȫ����������ʼDZ������Ա����ֽ�Ʒ����֪�ʼDZ�2Ԫ/�������Ա�1Ԫ/֧����ÿ�ֽ�Ʒ������1����
��1�����蹺��ʼDZ�x�������Ա�y֧��д��y��x֮��Ĺ�ϵʽ��
��2���ж����ֹ��������о����п��ܵĽ����
��3����������������ѡһ�ַ��������������Ա���ʼDZ�������ȵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬ����ѧΪ�ḻѧ����У������Ӿ�Ծ������Ʒ�̵�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ����������3�������2��������310Ԫ������2�������5��������500Ԫ��
��1������һ������һ������������Ԫ��
��2������ͬ����ѧ��ʵ���������Ӿ�Ծ������Ʒ�̵�һ���Թ������������96����Ҫ���������������ܷ��ò�����5720Ԫ��������ѧ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͭ��ְҵ����ѧԺ�ס�������ѧ���μӲ���������ѵ.����������ѵ�ڼ�μӵĶ�β��Գɼ��������ȡ8�Σ���¼���£�
ѧ�� | 8�β��Գɼ����֣� | ƽ���� | ��λ�� | ���� | |||||||
�� | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 | 85 | 35.5 | |
�� | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 | 84 | ||
(1)�����ڱ������ϼס�������ѧ����8�β��Գɼ���ƽ��������λ���ͷ��������ƽ�����ͷ���ļ���Ҫ�й��̣�.
(2)��Ҫ����ѡ��һ�˲μӲ������ܴ�������ͳ��ѧ�ĽǶȿ��ǣ�����Ϊѡ������ͬѧ�μӺ��ʣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com