
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.
初步感知:
(1)如图1,当点D在边BC上时,①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.
【答案】
(1)
①证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵∠DAF=60°,
∴∠BAC=∠DAF,
∴∠BAD=∠CAF,
∵四边形ADEF是菱形,
∴AD=AF,
在△ABD和△ACF中, 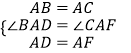 ,
,
∴△ABD≌△ACF(SAS),
∴∠ADB=∠AFC,
②解:∠AFC=∠ACB+∠DAC成立.理由如下:
∵△ABD≌△ACF,
∴∠ADB=∠AFC,
∵∠ADB=∠ACB+∠DAC,
∴∠AFC=∠ACB+∠DAC
问题探究:
(2)
解:∠AFC=∠ACB+∠DAC不成立.
∠AFC、∠ACB、∠DAC之间的等量关系是∠AFC=∠ACB﹣∠DAC.理由如下:
∵△ABC为等边三角形,
∴AB=AC,
∠BAC=60°,
∵∠BAC=∠DAF,
∴∠BAD=∠CAF,
∵四边形ADEF是菱形,
∴AD=AF.
在△ABD和△ACF中, 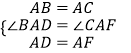 ,
,
∴△ABD≌△ACF(SAS).
∴∠ADB=∠AFC.
又∵∠ACB=∠ADC+∠DAC,
∴∠AFC=∠ACB﹣∠DAC
类比分析:
(3)
解:补全图形如图所示:
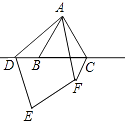
∠AFC、∠ACB、∠DAC之间的等量关系是:∠AFC+∠DAC+∠ACB=180°;理由如下:
同(2)得:△ABD≌△ACF,
∴∠ADC=∠AFC,
∵∠ADC+∠ACB+∠DAC=180°,
∴∠AFC+∠DAC+∠ACB=180°.
【解析】(1)①由AB=AC,AD=AF,∠BAD=∠CAF,按照SAS判断两三角形全等得出∠ADB=∠AFC;②由全等三角形的性质和三角形的外角性质即可得出结论;(2)此题应先判断得出正确的等量关系,然后再根据△ABD≌△ACF即可证明;(3)补全图形后由图形,由全等三角形的性质和三角形内角和定理即可得出∠AFC、∠ACB、∠DAC之间存在的等量关系.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG.
(1)发现
①线段DE、BG之间的数量关系是;
②直线DE、BG之间的位置关系是 .
(2)探究
如图2,将正方形AEFG绕点A逆时针旋转,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)应用
如图3,将正方形AEFG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=4,请直接写出点P到CD所在直线距离的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: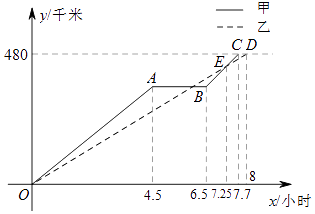
(1)由于汽车发生故障,甲车在途中停留了小时;
(2)甲车排除故障后,立即提速赶往景点.请问甲车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米,请通过计算说明,按图象所表示的走法是否符合约定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为 ![]() .
. 
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图: 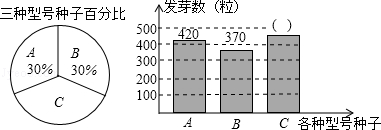
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com