
【题目】如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG.
(1)发现
①线段DE、BG之间的数量关系是;
②直线DE、BG之间的位置关系是 .
(2)探究
如图2,将正方形AEFG绕点A逆时针旋转,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)应用
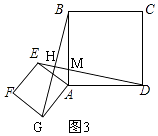
如图3,将正方形AEFG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=4,请直接写出点P到CD所在直线距离的最大值和最小值.
【答案】
(1)DE=BG;DE⊥BG
(2)
解:(1)中的结论仍然成立,理由是:
①如图3,∵四边形AEFG和四边形ABCD是正方形,
∴AE=AG,AD=AB,∠EAG=∠DAB=90°,
∴∠EAD=∠GAB=90°+∠EAB,
在△EAD和△GAB中,
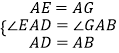 ,
,
∴△EAD≌△GAB(SAS),
∴ED=GB;
②ED⊥GB,
理由是:∵△EAD≌△GAB,
∴∠GBA=∠EDA,
∵∠AMD+∠ADM=90°,∠BMH=∠AMD,
∴∠BMH+∠GBA=90°,
∴∠DHB=180°﹣90°=90°,
∴ED⊥GB;
(3)
解:应用
将正方形AEFG绕点A逆时针旋转一周,即点E和G在以A为圆心,以2为半径的圆上,
过P作PH⊥CD于H,
①当P与F重合时,此时PH最小,如图4,

在Rt△AED中,AD=4,AE=2,
∴∠ADE=30°,DE= ![]() =2
=2 ![]() ,
,
∴DF=DE﹣EF=2 ![]() ﹣2,
﹣2,
∵AD⊥CD,PH⊥CD,
∴AD∥PH,
∴∠DPH=∠ADE=30°,
cos30°= ![]() =
= ![]() ,
,
∴PH= ![]() (2
(2 ![]() ﹣2)=3﹣
﹣2)=3﹣ ![]() ;
;
②∵DE⊥BG,∠BAD=90°,
∴以BD的中点O为圆心,以BD为直径作圆,P、A在圆上,
当P在 ![]() 的中点时,如图5,此时PH的值最大,
的中点时,如图5,此时PH的值最大,
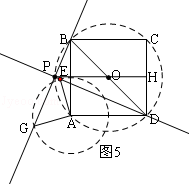
∵AB=AD=4,
由勾股定理得:BD=4 ![]() ,
,
则半径OB=OP=2 ![]()
∴PH=2+2 ![]() .
.
综上所述,点P到CD所在直线距离的最大值是2+2 ![]() ,最小值是3﹣
,最小值是3﹣ ![]() .
.
【解析】解:(1)发现①线段DE、BG之间的数量关系是:DE=BG,
理由是:如图1,∵四边形ABCD是正方形,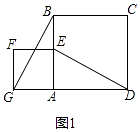
∴AB=AD,∠BDA=90°,
∴∠BAG=∠BAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,
∴△AED≌△AGB,
∴DE=BG;②直线DE、BG之间的位置关系是:DE⊥BG,
理由是:如图2,延长DE交BG于Q,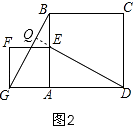
由△AED≌△AGB得:∠ABG=∠ADE,
∵∠AED+∠ADE=90°,∠AED=∠BEQ,
∴∠BEQ+∠ABG=90°,
∴∠BQE=90°,
∴DE⊥BG;
所以答案是:①DE=BG;②DE⊥BG;
【考点精析】关于本题考查的图形的旋转,需要了解每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能得出正确答案.


科目:初中数学 来源: 题型:
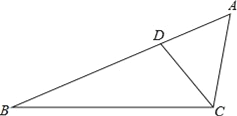
【题目】如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: 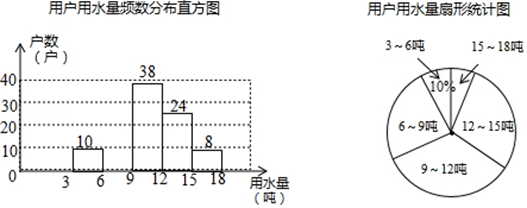
(1)此次抽样调查的样本容量是;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与反比例函数y= ![]() 的图形交于A(a,4)和B(4,1)两点.
的图形交于A(a,4)和B(4,1)两点. 
(1)求b,k的值;
(2)在第一象限内,当一次函数y=﹣x+b的值大于反比例函数y= ![]() 的值时,直接写出自变量x的取值范围;
的值时,直接写出自变量x的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线只有一个交点时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神奇的数学世界是不是只有锻炼思维的数字游戏?每天都在面对繁杂的数字计算?答案当然是否定的,曼妙的数学畅游在迷人的数字和丰富多彩的图形之间,将数与形巧妙地融汇在一起,不可分割.我们都知道,实数与数轴上的点一一对应,数轴上的线段可以由端点所对应的实数确定,这是一维的数与形;增加到两条数轴,可以形成平面直角坐标系,这样有序数对与平面内的点一一对应,平面内的多边形及其内容可以由多边形的边上所有点的坐标所确定,这是二维的数与形.而在平面直角坐标系中的图形更是神秘,在平面内任意画一条(或多条)曲线(或直线),它(们)把平面分割成的部分都称为区域,特别地,如果曲线首尾相接,那么形成的有限部分也称为封闭区域.如何研究这些区域呢?当然离不开数,我们可以通过区域内点的坐标规律来刻画图形.反过来,我们也可以根据点坐标的规律在平面直角坐标系内找到它们,画出相应的图形.聪明的你看懂了吗?试着做做看.
(1)分别解不等式![]() 和
和![]() ,并把不等式的解集画在同一个数轴上;
,并把不等式的解集画在同一个数轴上;
(2)点P(x,y)在平面直角坐标系的第一象限,并且横坐标与纵坐标分别满足不等式![]() 和
和![]() ,请画出满足条件的点P所在的最大区域,并求出区域的面积;
,请画出满足条件的点P所在的最大区域,并求出区域的面积;
(3)去掉(2)中“点P在第一象限”这个条件,其余条件保持不变,求满足条件的点P所在最大区域与平面直角坐标系第二、四象限角平分线所围成封闭区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.
初步感知:
(1)如图1,当点D在边BC上时,①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com