
【题目】神奇的数学世界是不是只有锻炼思维的数字游戏?每天都在面对繁杂的数字计算?答案当然是否定的,曼妙的数学畅游在迷人的数字和丰富多彩的图形之间,将数与形巧妙地融汇在一起,不可分割.我们都知道,实数与数轴上的点一一对应,数轴上的线段可以由端点所对应的实数确定,这是一维的数与形;增加到两条数轴,可以形成平面直角坐标系,这样有序数对与平面内的点一一对应,平面内的多边形及其内容可以由多边形的边上所有点的坐标所确定,这是二维的数与形.而在平面直角坐标系中的图形更是神秘,在平面内任意画一条(或多条)曲线(或直线),它(们)把平面分割成的部分都称为区域,特别地,如果曲线首尾相接,那么形成的有限部分也称为封闭区域.如何研究这些区域呢?当然离不开数,我们可以通过区域内点的坐标规律来刻画图形.反过来,我们也可以根据点坐标的规律在平面直角坐标系内找到它们,画出相应的图形.聪明的你看懂了吗?试着做做看.
(1)分别解不等式![]() 和
和![]() ,并把不等式的解集画在同一个数轴上;
,并把不等式的解集画在同一个数轴上;
(2)点P(x,y)在平面直角坐标系的第一象限,并且横坐标与纵坐标分别满足不等式![]() 和
和![]() ,请画出满足条件的点P所在的最大区域,并求出区域的面积;
,请画出满足条件的点P所在的最大区域,并求出区域的面积;
(3)去掉(2)中“点P在第一象限”这个条件,其余条件保持不变,求满足条件的点P所在最大区域与平面直角坐标系第二、四象限角平分线所围成封闭区域的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
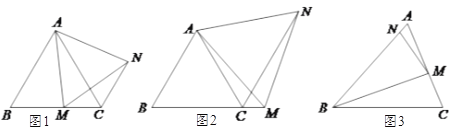
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是AB边的中点,以AE为边作正方形AEFG,连接DE,BG.
(1)发现
①线段DE、BG之间的数量关系是;
②直线DE、BG之间的位置关系是 .
(2)探究
如图2,将正方形AEFG绕点A逆时针旋转,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)应用
如图3,将正方形AEFG绕点A逆时针旋转一周,记直线DE与BG的交点为P,若AB=4,请直接写出点P到CD所在直线距离的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为x1 , 第二个三角形数记为x2 , …第n个三角形数记为xn , 则xn+xn+1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
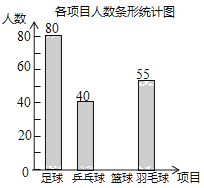
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com