
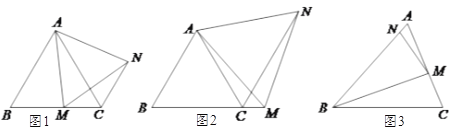
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
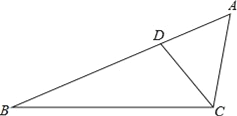
【题目】如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( ) 
A.(4,2 ![]() )
)
B.(3,3 ![]() )
)
C.(4,3 ![]() )
)
D.(3,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.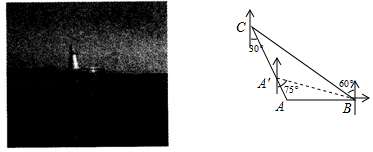
(1)求出此时点A到点C的距离;
(2)若小明从A处沿AC方向向C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: 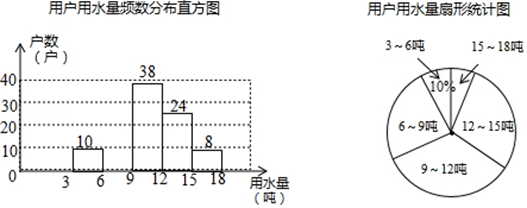
(1)此次抽样调查的样本容量是;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神奇的数学世界是不是只有锻炼思维的数字游戏?每天都在面对繁杂的数字计算?答案当然是否定的,曼妙的数学畅游在迷人的数字和丰富多彩的图形之间,将数与形巧妙地融汇在一起,不可分割.我们都知道,实数与数轴上的点一一对应,数轴上的线段可以由端点所对应的实数确定,这是一维的数与形;增加到两条数轴,可以形成平面直角坐标系,这样有序数对与平面内的点一一对应,平面内的多边形及其内容可以由多边形的边上所有点的坐标所确定,这是二维的数与形.而在平面直角坐标系中的图形更是神秘,在平面内任意画一条(或多条)曲线(或直线),它(们)把平面分割成的部分都称为区域,特别地,如果曲线首尾相接,那么形成的有限部分也称为封闭区域.如何研究这些区域呢?当然离不开数,我们可以通过区域内点的坐标规律来刻画图形.反过来,我们也可以根据点坐标的规律在平面直角坐标系内找到它们,画出相应的图形.聪明的你看懂了吗?试着做做看.
(1)分别解不等式![]() 和
和![]() ,并把不等式的解集画在同一个数轴上;
,并把不等式的解集画在同一个数轴上;
(2)点P(x,y)在平面直角坐标系的第一象限,并且横坐标与纵坐标分别满足不等式![]() 和
和![]() ,请画出满足条件的点P所在的最大区域,并求出区域的面积;
,请画出满足条件的点P所在的最大区域,并求出区域的面积;
(3)去掉(2)中“点P在第一象限”这个条件,其余条件保持不变,求满足条件的点P所在最大区域与平面直角坐标系第二、四象限角平分线所围成封闭区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com