
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

【答案】(1)a;(2)2a;(3)6a;(4)0.5a.
【解析】
(1)根据阅读材料中所得结论易得S1=a;
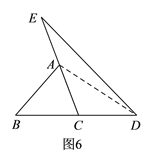
(2)如图6,连接AD,由阅读材料中中所得结论结合已知条件易得S△ADE=S△ACD=S△ABC=a,由此可得S2=2a;
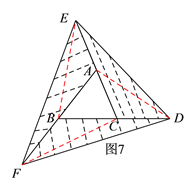
(3)如图7,连接AD、BE、CF,由(2)中结论可得S△CDE=2a,S△AEF=2a,S△BDF=2a,然后由S3= S△CDE+S△AEF+S△BDF即可求得S3=6a;
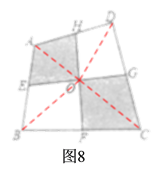
(4)如图8,连接OA、OB、OC、OD,则由阅读材料中的结论可得:S△AOE=![]() S△AOB,S△AOH=
S△AOB,S△AOH=![]() S△AOD,S△COF=
S△AOD,S△COF=![]() S△BOC,S△COG=
S△BOC,S△COG=![]() S△COD,将上述等式相交即可得到S阴影=
S△COD,将上述等式相交即可得到S阴影=![]() S四边形ABCD=
S四边形ABCD=![]() .
.
(1)如图2,由题意可得:在△ABD中,AC是BD边上的中线,
∴S1=S△ACD=S△ABC=a;
(2)如图6,连接AD,则由题意可知,AD是△CDE的边CE上的中线,
∴S△ADE=S△ACD,
又∵S△ACD=S△ABC=a ,
∴S2= S△ADE+S△ACD=2a;
(3)如图7,连接AD、BE和CF,则由(2)中结论可得:
S△CDE=2a,S△AEF=2a,S△BDF=2a,
∵S3= S△CDE+S△AEF+S△BDF,
∴S3=2a+2a+2a=6a;
(4)如图8,连接连接OA、OB、OC、OD,
∵点E、F、G、H分别是四边形ABCD四边的中点,
∴S△AOE=![]() S△AOB,S△AOH=
S△AOB,S△AOH=![]() S△AOD,S△COF=
S△AOD,S△COF=![]() S△BOC,S△COG=
S△BOC,S△COG=![]() S△COD,
S△COD,
∴S阴影=S△AOE+S△AOH+S△COF+S△COG
=![]() S△AOB+
S△AOB+![]() S△AOD+
S△AOD+![]() S△BOC+
S△BOC+![]() S△COD
S△COD
=![]() S四边形ABCD
S四边形ABCD
=![]() .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为平面内一点.
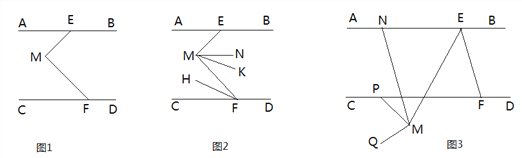
(1)如图1,∠AEM,∠M,∠CFM的数量关系为 ;(直接写出答案)
(2)如图2,∠AEM=48°,MN平分∠EMF,FH平分∠MFC,MK∥FH,求∠NMK的度数;
(3)如图3,点P为CD上一点,∠BEF=n·∠MEF,∠PMQ=n·∠PME,过点M作MN∥EF交AB于点N,请直接写出∠PMQ,∠BEF,∠PMN之间的数量关系.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
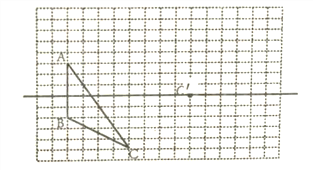
【题目】如图,方格纸中每个小正方形的边长都为l.在方格纸中将三角形ABC经过一次平移后得到三角形A'B'C’,图中标出了点C的对应点C'.
(1)请画出平移后的三角形A'B'C’;
(2)连接AA’,CC’,则这两条线段之间的关系是 ;
(3)建立合适的平面直角坐标系,并写出A'、B'、C'的坐标;
(4)三角形A'B'C'的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC. 
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣ ![]() ,求⊙O的半径和BF的长.
,求⊙O的半径和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
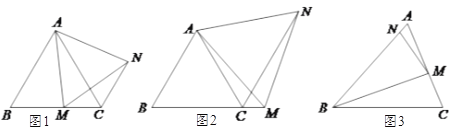
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个不相等的有理数a,b,我们规定符号![]() 表示a,b中的较大值,如
表示a,b中的较大值,如![]() ,
,![]() ,请解答下列问题:
,请解答下列问题:
(1)![]() _______________;
_______________;
(2)如果![]() ,求x的取值范围;
,求x的取值范围;
(3)如果![]() ,求x的值
,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( ) 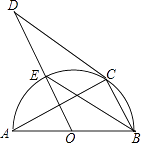
A.AC⊥BC
B.BE平分∠ABC
C.BE∥CD
D.∠D=∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
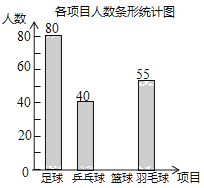
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com