
【题目】对于两个不相等的有理数a,b,我们规定符号![]() 表示a,b中的较大值,如
表示a,b中的较大值,如![]() ,
,![]() ,请解答下列问题:
,请解答下列问题:
(1)![]() _______________;
_______________;
(2)如果![]() ,求x的取值范围;
,求x的取值范围;
(3)如果![]() ,求x的值
,求x的值
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. 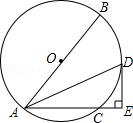
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系为:____________________(直接写出结果).
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP,CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系为:____________________(直接写出结果).
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com