
【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( ) 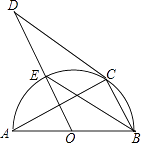
A.AC⊥BC
B.BE平分∠ABC
C.BE∥CD
D.∠D=∠A
【答案】C
【解析】解:连接OC. ∵AB是直径,
∴∠ACB=90°,
∴AC⊥BC,故A正确,
∵OD∥BC,
∴∠EBC=∠BEO,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠EBO=∠EBC,
∴BE平分∠ABC,故B正确,
∵DC是切线,
∴DC⊥CO,
∴∠DCO=90°,
∴∠D+∠DOC=90°,
∵BC⊥AC,OD∥BC,
∴OD⊥AC,
∵OA=OC,
∴∠AOD=∠DOC,
∴∠A+∠AOD=90°,
∴∠A=∠D,故D正确.
无法判断C正确,
故选C.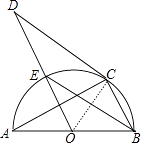
【考点精析】关于本题考查的切线的性质定理,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( ) 
A.(4,2 ![]() )
)
B.(3,3 ![]() )
)
C.(4,3 ![]() )
)
D.(3,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: 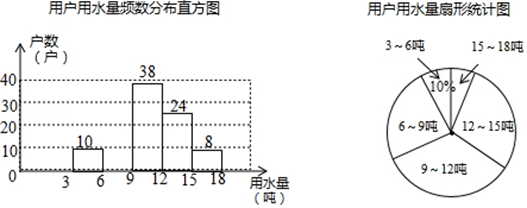
(1)此次抽样调查的样本容量是;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
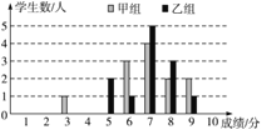
【题目】(8分)一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分为优秀.这次测验中甲、乙两组学生成绩分布的条形统计图如图.
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com