
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

【答案】2.5
【解析】试题分析:∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,∴DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°,∵∠EDF=45°,∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,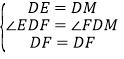 ,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM﹣MF=BM﹣EF=4﹣x,
∵EB=AB﹣AE=3﹣1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2, 即22+(4﹣x)2=x2,
解得:x=![]() , ∴FM=
, ∴FM=![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.

【答案】(1)60°.AD=BE;(2)AB=17;(3)∠AOE的度数是60°或120°.
【解析】试题分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由(1)知△ACD≌△BCE,得∠CAD=∠CBE,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.
试题解析:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
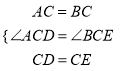 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
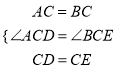 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE=AE-DE=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC∠CED=90°.
∴AB=![]() =17;
=17;
(3)由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°
∴∠AOE=180°120°=60°,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
点睛:本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力.
【题型】解答题
【结束】
26
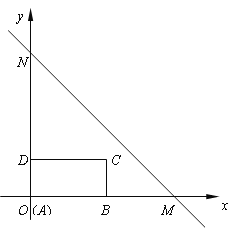
【题目】如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴上,AB=2,AD=1.长方形ABCD由点A与点O重合的位置开始,以每秒1个单位长度的速度沿x轴正方向作匀速直线运动,当点A与点M重合时停止运动.设长方形运动的时间为t秒,长方形ABCD与△OMN重合部分的面积为S.
(1)求直线MN的解析式;
(2)当t=1时,请判断点C是否在直线MN上,并说明理由;
(3)请求出当t为何值时,点D在直线MN上;
(4)直接写出在整个运动过程中S与t的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
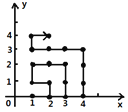
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2), (2,2)···根据这个规律,第140个点的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB∥CD,点E,F分别在直线AB,CD上,点M为平面内一点.
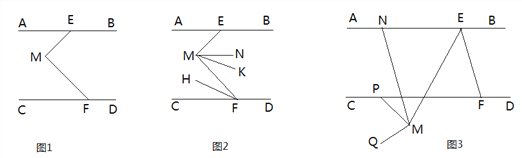
(1)如图1,∠AEM,∠M,∠CFM的数量关系为 ;(直接写出答案)
(2)如图2,∠AEM=48°,MN平分∠EMF,FH平分∠MFC,MK∥FH,求∠NMK的度数;
(3)如图3,点P为CD上一点,∠BEF=n·∠MEF,∠PMQ=n·∠PME,过点M作MN∥EF交AB于点N,请直接写出∠PMQ,∠BEF,∠PMN之间的数量关系.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
查看答案和解析>>
科目:初中数学 来源: 题型:
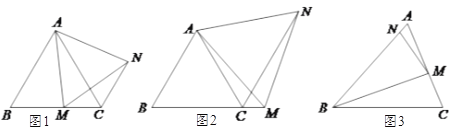
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com