
����Ŀ����1�����ⷢ�֣���ͼ1����ACB����DCE��Ϊ�ȱ������Σ�����DCE��ת����A��D��E��ͬһֱ���ϣ�����BE��
��գ��� ��AEB�Ķ���Ϊ_______�����߶�AD��BE֮���������ϵ��______��
��2����չ�о���
��ͼ2����ACB����DCE��Ϊ���������Σ��ҡ�ACB=��DCE=90������A��D��E��ͬһֱ���ϣ���AE=15��DE=7����AB�ij��ȣ�
��3��̽�����֣�
ͼ1�е���ACB����DCE������DCE��ת�����е���A��D��E����ͬһֱ����ʱ����ֱ��AD��BE�ཻ�ڵ�O�����ڱ���ͼ��̽����AOE�Ķ�����ֱ��д�����������˵�����ɣ�

���𰸡���1��60����AD=BE����2��AB=17����3����AOE�Ķ�����60����120����
�������������������1����������֤��ACD�ա�BCE���Ӷ��õ���AD=BE����ADC=��BEC���ɵ�A��D��E��ͬһֱ���Ͽ������ADC���Ӷ����������AEB�Ķ�����
��2�����գ�1���еĽⷨ�������AEB�Ķ�����֤��AD=BE������DCEΪ����ֱ�������μ�CMΪ��DCE��DE���ϵĸ߿ɵ�CM=DM=ME���Ӷ�֤��AE=2CH+BE��
��3���ɣ�1��֪��ACD�ա�BCE���á�CAD=��CBE���ɡ�CAB=��ABC=60������֪��EAB+��ABE=120�������������ε��ڽǺͶ�����֪��AOE=60����
�����������1��������ACB����DCE��Ϊ�ȱ������Σ�
��CA=CB��CD=CE����ACB=��DCE=60��.
���ACD=��BCE.
����ACD����BCE��
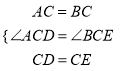 ��
��
����ACD����BCE(SAS).
���ADC=��BEC.
����DCEΪ�ȱ������Σ�
���CDE=��CED=60��.
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=120��.
���BEC=120��.
���AEB=��BEC��CED=60��.
�ʴ�Ϊ��60��.
�ڡ���ACD����BCE��
��AD=BE.
�ʴ�Ϊ��AD=BE.
��2������ACB����DCE��Ϊ����ֱ�������Σ�
��CA=CB��CD=CE����ACB=��DCE=90��.
���ACD=��BCE.
����ACD����BCE��
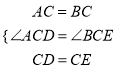 ��
��
����ACD����BCE(SAS).
��AD=BE=AE-DE=8����ADC=��BEC��
����DCEΪ����ֱ����������
���CDE=��CED=45��.
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=135��.
���BEC=135��.
���AEB=��BEC��CED=90��.
��AB=![]() =17��
=17��
��3������1��֪��ACD����BCE��
���CAD=��CBE��
�ߡ�CAB=��CBA=60����
���OAB+��OBA=120��
���AOE=180��120��=60����
ͬ����á�AOB=60����
���AOE=120����
���AOE�Ķ�����60����120��.
�㾦�����⿼���˵ȱ������ε����ʡ����������ε����ʡ�ֱ��������б���ϵ����ߵ���б�ߵ�һ�롢������ȫ�ȵ��ж������ʵ�֪ʶ���������������е�֪ʶ�;��������������.
�����͡������
��������
26
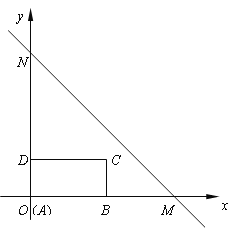
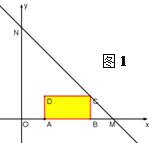
����Ŀ����ͼ��ֱ��MN��y����x��b��x�ύ�ڵ�M��4��0������y�ύ�ڵ�N��������ABCD�ı�AB��x���ϣ�AB��2��AD��1��������ABCD�ɵ�A���O�غϵ�λ�ÿ�ʼ����ÿ��1����λ���ȵ��ٶ���x��������������ֱ���˶�������A���M�غ�ʱֹͣ�˶����賤�����˶���ʱ��Ϊt�룬������ABCD���OMN�غϲ��ֵ����ΪS��
��1����ֱ��MN�Ľ���ʽ��
��2����t��1ʱ�����жϵ�C�Ƿ���ֱ��MN�ϣ���˵�����ɣ�
��3���������tΪ��ֵʱ����D��ֱ��MN�ϣ�
��4��ֱ��д���������˶�������S��t�ĺ�����ϵʽ
���𰸡���1��y=-x+4��2��t=1ʱ����C��3��1����ֱ��MN����3��t=3ʱ����D��ֱ��MN����4��S=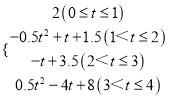
�������������������1���ѵ�![]() ��4��0������ֱ��
��4��0������ֱ��![]() ������ý����
������ý����
��2���������![]() =1ʱ��A�˶���·�̣����ɵõ���C�����꣬�ٴ���ֱ��MN�Ľ���ʽ�����жϣ�
=1ʱ��A�˶���·�̣����ɵõ���C�����꣬�ٴ���ֱ��MN�Ľ���ʽ�����жϣ�
��3���ȵõ��˶���ʼʱ��D���꣬����![]() ���õ���ʱ��D�����꼴���жϣ�
���õ���ʱ��D�����꼴���жϣ�
��4����![]() ��
��![]() ��
��![]() ��
��![]() ���������������.
���������������.
��1����ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��4��0��
��4��0��
��![]() �����
�����![]()
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��2����ͼ1����![]() =1ʱ����
=1ʱ����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
��![]() =1ʱ����A�˶���·��ΪAO=1��1=1��
=1ʱ����A�˶���·��ΪAO=1��1=1��
����![]() ��
�� ![]()
����ʱ��C������Ϊ��3��1��
�ѵ�C���������ֱ��MN�Ľ���ʽ![]()
��![]()
����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
��3����ͼ2����![]() ����ƽ�ƹ����������겻��
����ƽ�ƹ����������겻��

������֪���˶���ʼʱ��D����Ϊ��0��1��
��![]() �����
�����![]()
��ʱ��D������Ϊ��3��1��
��![]() ��
��
��![]() =3ʱ����
=3ʱ����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
��4��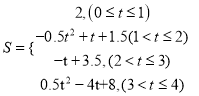 .
.


 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AB��CD
��1����ͼ1����E��ֱ��BD����࣬�����ABE����CDE����BED��������ϵ����֤����Ľ��ۣ�
��2����ͼ2����E��ֱ��BD����࣬BF��DF�ֱ�ƽ�֡�ABE����CDE�������BFD�͡�BED��������ϵ����֤����Ľ��ۣ�
��3����ͼ3����E��ֱ��BD���Ҳ࣬BF��DF�ֱ�ƽ�֡�ABE����CDE����ô�ڣ�2�����С�BFD�͡�BED��������ϵ�IJ����Ƿ��Գ����������������֤�����������������д����IJ��룬��֤����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2��A�ͳ���1��B�ͳ���������һ�ο��˻�10��.��1��A�ͳ���2��B�ͳ���������һ�ο��˻�11��.ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�a����B�ͳ�b��,һ�����꣬��ÿ���������ػ���.����������Ϣ����������⣺
��1��1��A�ͳ���1��B�ͳ���������һ�ηֱ���˻�����ٶ֣�
��2�������������˾��������
��3����A�ͳ�ÿ�������ÿ��100Ԫ��B�ͳ�ÿ�������ÿ��120Ԫ.��ѡ����ʡǮ�����������������ٵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���ACB��90�㣬CD��AB������Ϊ��D����֪AC��3��BC��4.

(1)�߶�AD��CD��CD��BD�Dz��dzɱ����߶Σ�д��������ɣ�
(2)�����ͼ���У��ܷ����ҳ������ɱ����������߶Σ�����ܣ�������д�����飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�飺 ![]() ������������գ���ɱ���Ľⷨ��
������������գ���ɱ���Ľⷨ��
![]()
��1���ⲻ��ʽ��1������________��
��2���ⲻ��ʽ��2������________��
��3���Ѳ���ʽ ��1���� ��2���Ľ⼯�������ϱ�ʾ������
��4��ԭ����ʽ�Ľ⼯Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪������ϵ�У�A��B��D���������ֱ�ΪA��8��0����B��0��4����D����1��0������C���B����x��Գƣ�����AB��AC��
��1�����A��B��D����������ߵĽ���ʽ��
��2����һ����E��ԭ��O��������ÿ��2����λ���ٶ������˶�������E��x��Ĵ��ߣ����������ڵ�P�����߶�CA�ڵ�M������PA��PB�����E�˶���ʱ��Ϊt��0��t��4���룬���ı���PBCA�����S��t�ĺ�����ϵʽ��������ı���PBCA����������
��3�������ߵĶԳ������Ƿ����һ��H��ʹ�á�ABH��ֱ�������Σ������ڣ���ֱ��д����H�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ����y��Ķ�ֱ��a�ı���ʽΪx=t��ֱ��b�ı���ʽΪy=x��ֱ��c�ı���ʽΪy=��![]() x+2���Ҷ�ֱ��a�ֱ�ֱ��b��c�ڵ�D��E��E��D���Ϸ�����P��y����һ�����㣬��������PDE�ǵ���ֱ�������Σ����P��������________��
x+2���Ҷ�ֱ��a�ֱ�ֱ��b��c�ڵ�D��E��E��D���Ϸ�����P��y����һ�����㣬��������PDE�ǵ���ֱ�������Σ����P��������________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ3��E��F�ֱ���AB��BC���ϵĵ㣬����EDF=45��������DAE�Ƶ�D��ʱ����ת90�����õ���DCM����AE=1����FM�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
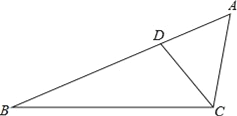
����Ŀ����ͼ����D����ABC��AB���ϣ��ҡ�ACD=��A��
��1������BDC��ƽ����DE����BC�ڵ�E���ó߹���ͼ����������ͼ�ۼ�����Ҫ��д��������
��2���ڣ�1���������£��ж�ֱ��DE��ֱ��AC��λ�ù�ϵ����Ҫ��֤������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com