【题目】甲乙两人做掷一个均匀小立方体的游戏，立方体的每个面上分别标有数字1，2，3，4，5，6，任意掷出小立方体后，若朝上的数字小于3，则甲获胜；若朝上的数字大于3 ，则乙获胜．你认为这个游戏对甲乙双方公平吗？为什么？你能不能就上面的小立方体设计一个较为公平的游戏？
科学实验活动册系列答案科目：初中数学 来源： 题型：
【题目】如图，一次函数y=kx+b与反比例函数
的图象交于点A（1，6），B（3，n）两点．
（1）求一次函数的表达式；
（2）在y轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“绿水青山，就是金山银山”．某旅游景区为了保护环境，需购买
两种型号的垃圾处理设备共10台，已知每台
型设备日处理能力为12吨；每台
型设备日处理能力为15吨，购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买两种设备的方案；
(2)已知每台型设备价格为3万元，每台型设备价格为4.4万元.厂家为了促销产品，规定货款不低于40万元时，则按9折优惠；问:采用(1)设计的哪种方案，使购买费用最少，为什么?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（ ）
A. 4：2：1 B. 5：3：1 C. 25：12：5 D. 51：24：10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.
（1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .
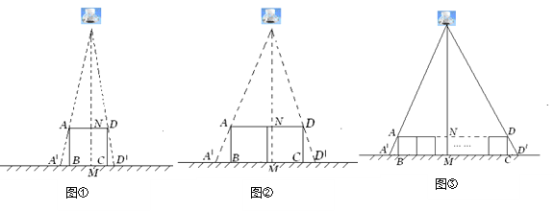（2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？
（3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABD中，C为BD上一点，使得CA＝CD，过点C作CE∥AD交AB于点E，过点D作DF⊥AD交AC的处长线于点F．
（1）若CD＝3，求AF的长；
（2）若∠B＝30°，∠ADC＝40°，求证：AC＝EC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是1、4、25．则△ABC的面积是 ．
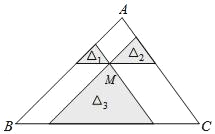
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，AC=BC，CD=CE，∠ACB=∠DCE=α，AD、BE相交于点M，连接CM．
（1）求证：BE=AD；并用含α的式子表示∠AMB的度数；
（2）当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图2，判断△CPQ的形状，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从谢家集到田家庵有3路，121路，26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间，在每条线路上随机选取了450个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下:
用时的频数 用时 线路 |
|
|
| 合计 |
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
早高峰期间，乘坐__________（“3路”,“121路”或“26路”）线路上的公交车，从谢家集到田家庵“用时不超过50分钟”的可能性最大．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
