
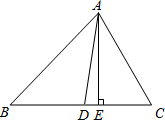
 △ABC中,AD、AE分别为角平分线和高,若∠B=60°,∠C=70°,求∠DAE.
△ABC中,AD、AE分别为角平分线和高,若∠B=60°,∠C=70°,求∠DAE. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 保证“神舟九号”载人飞船成功发射,对重要零部件的检查 | |
| B. | 了解人们对环境保护的意识 | |
| C. | 了解一批灯泡的使用寿命 | |
| D. | 了解央视2013年“春节联欢晚会”栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
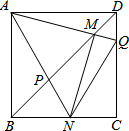 如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.
如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 400.47(1+x)2=467.12 | B. | 467.12(1+x)2=400.47 | ||
| C. | 400.47(1+2x)2=467.12 | D. | 467.12(1+2x)2=400.47 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
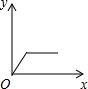 如图是反应两个变量关系的图,下列的四个情境比较适合该图的是( )
如图是反应两个变量关系的图,下列的四个情境比较适合该图的是( )| A. | 一辆汽车从起动到匀速行驶,速度与时间的关系 | |
| B. | 一杯热水放在桌子上,它的水温与时间的关系 | |
| C. | 一架飞机从起飞到降落的速度与时间的关系 | |
| D. | 一个踢出的足球的速度与时间的关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
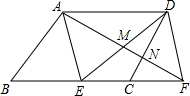 在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.
在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com